* مطالب علمی *
ایساتیس
آقاشیر
.: شهر عشق :.
جملات زیبا
تعقل و تفکر
دکتر رحمت سخنی
بیگانه ، دختری در میان مردمان
تا ریشه هست، جوانه باید زد...
اس ام اس عاشقانه
خاطرات خاشعات
اس ام اس سرکاری اس ام اس خنده دار و اس ام اس طنز
وسوسه عقل
پرهیزکار عاشق است !
فروش و تعمیر موبایل در استان یزد
آموزش
وبلاگ تخصصی کامپیوتر
هک و ترفند
فروش و تعمیر موبایل در استان یزد
انجمن فیزیک پژوهش سرای بشرویه
عاشقان خدا فراری و گریزان به سوی عشق و حق®
وبلاگ عشق و محبت ( اقا افشین)
باید زیست
دست نوشته های دو میوه خوشمزه
در دل نهفته ها
روزگاران(حتما یه سری بهش بزن ضرر نمی کنی)
فقط برای ادد لیستم...سند تو ال
تجربه های مدیریت
سولات تخصصی امتحان دکترا دانشگاه آزاد
سولات تخصصی امتحان دکترا دانشگاه آزاد
ارزانترین و بزرگترین مرکز سوالات آزمون دکترا
عکس و اس ام اس عشقولانه
دانلود نرم افزار های روز دنیا
شاهرخ
مکانیک هوافضا اخترفیزیک
مکانیک ، هوافضا ،اخترفیزیک
وبلاگ تخصصی فیزیک و اختر فیزیک
وبلاگ تخصصی فیزیک جامدات
همه با هم برای از بین نرفتن فرهنگ ایرانی
انتخاب
فیزیک و واقعیت
ترجمه متون کوتاه انگلیسی
دنیای بیکران فیزیک
مقدمه
در زمین نواحی وجود دارند که در آنجا مؤلفههای مغناطیسی بطور ناگهانی تغییر میکنند و مقادیری به خود میگیرند که با مقادیر مربوط به محلهای مجاور تفاوت فاحشی دارند. این نواحی ، نواحی با ناهنجارهای مغناطیسی نامیده میشود. در اغلب موارد ناهنجاری مغناطیسی ناشی از فشار توده بزرگی از سنگ آهنهای مغناطیسی در زیر سطح زمین است. به این دلیل مطالعه ناهنجاریهای مغناطیسی اطلاعات با ارزشی در مورد وجود و محل مخازن و سنگهای مغناطیسی ارائه میدهند.
مغناطیس سنجی در کاوش منابع معدنی
یکی از بزرگترین و بهترین مطالعات در مورد ناهنجاریهای مغناطیسی شوروی سابق در ناهنجاری مغناطیسی کورسک (kurs توسط گروهی از فیزیکدانان روسی به سرپرستی لازارف (La-zarev) انجام گرفته و در آنجا مخازن سنگ عظیمی کشف شده است. تحلیل دقیق میدان مغناطیسی زمین وسیله توانمندی برای بررسی ذخایر معدنی زمین است. در حال حاضر جستجوی مغناطیس سنجی ، روش ژئوفیزیکی مهم و گستردهای است که برای اکتشافات معدنی بکار میرود.
مؤلفههای میدان مغناطیسی زمین در هر نقطه کره زمین با مرور زمان به آرامی تغییر میکند. بعضی از رصدخانههای مغناطیسی اروپایی اطلاعات جمع آوری شده در 300 تا 400 سال اخیر را در اختیار دارند. این اطلاعات تصور روشنی را در مورد قانون این تغییرات کند (قانون سدهای میدان مغناطیسی زمین) ارائه میدهند. ولی افزون بر تغییر سدهای میدان مغناطیسی زمین ، مؤلفههای میدان مغناطیسی زمین تغییرات دورهای جزئی در ضمن روز و سال نیز دارند. این تغییرات روزانه و سالانه مؤلفههای میدان مغناطیسی زمین مرسومند و معمولا کوچک هستند.
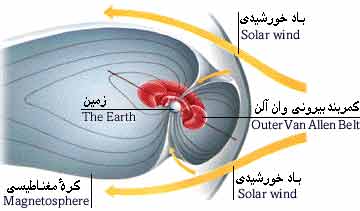 |
آشفتگی مغناطیسی
تمام این تغییرات دورهای در میدان مغناطیس تا اندازهای آرام صورت میگیرد. ولی ، گاهی میدان مغناطیسی زمین در مدت چند ساعت تغییرات ناگهانی و زیادی پیدا میکند. این پدیده توفان مغناطیسی یا آشفتگی مغناطیسی نامیده میشود. توفان مغناطیسی معمولا از 6 تا 12 ساعت طول میکشد و پس از آن مؤلفههای مغناطیسی زمین به تدریج مقادیر معلوم خود را به دست میآورند. در مواقع اعتدال (اعتدال بهاری یا اعتدال پاییزی) توفانهای مغناطیسی بیشتر از سایر دورههای سال مشاهده می شود.
دوره تناوب توفانهای مغناطیسی
تعداد و شدت توفانهای مغناطیسی از سالی نسبت به سال دیگر تغییر میکند. دورههای قلههای توفان مغناطیسی در فاصله 11.5 سال تکرار میشوند. پس از هر قله ، تعداد توفانهای مغناطیسی به تدریج کاهش مییابند و به مقدار مینیمم خود میرسند و دوباره تا مقدار قله زیاد میشوند. تعدادی از پدیدههای دیگر نیز شفقهای قطبی ، لکههای خورشیدی ، بعضی پدیدههای مربوط به انتشار امواج رادیویی و غیره) دارای دوره 11.5 سال هستند. امروزه میتوان اظهار داشت که این تطابقها تصادفی نیستند بلکه ارتباط ذاتی این پدیدهها را نشان میدهند.
کلمات کلیدی: مغناطیس
 |
اطلاعات اولیه
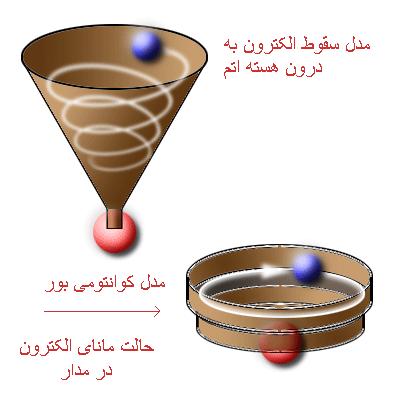
در بررسی ساختار اتم مدلهای مختلفی ارائه شده است. ابتداییترین این مدلها ، مدل سیارهای رادرفورد است. بعد از مدل سیارهای رادرفورد ، نیلز بوهر مدل جدیدی را ارائه داد (مدل اتمی بوهر). این مدل میتوانست ساختار طیفی اتم هیدروژن را توضیح دهد. در اصل موضوع بوهر که اساس و مبنای مدل بوهر است، فرض میشود که الکترونها مقیدند در مدارهایی حرکت کنند که در آنها اندازه حرکت الکترون مضرب درستی از h/2π باشد که h ثابت پلانک است. همچنین در این مدل فرض میشود که ترازهای انرژی کوانتیدهاند. بعدها که ساختار طیف مربوط به عناصر مختلف مورد توجه قرار گرفت، انرژی هر الکترون در اتم با یک سری اعداد که به عنوان اعداد کوانتومی معروف هستند، مشخص کردند.
اعداد کوانتومی اصلی
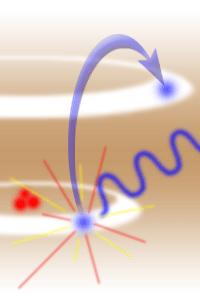
گفتیم که ترازهای انرژی در اتم گسسته هستند. این امر به این معنی است که اگر اتم توسط تابش الکترومغناطیسی بمباران شود، تابش توسط الکترونها جذب میشود. لذا الکترونها از ترازهای اولیه یا پایه خود تحریک شده و به ترازهای برانگیخته میروند، اما چون این حالت یک حالت ناپایدار است، لذا الکترون با گسیل تابش از تراز برانگیخته به تراز اولیه خود برمیگردد. مقدار انرژی جذب شده یا گسیل شده متناسب با فاصله ترازهای انرژی است، یعنی اگر انرژی تراز اولیه را با E و انرژی تراز برانگیخته را با ΄E مشخص کنیم، در این صورت فرکانس نور گسیل شده یا تحریک شده از رابطه E - E΄ = hv حاصل میشود.
از طرف دیگر ، چون طبق اصل موضوع بوهر ، اندازه حرکت الکترون باید مضرب صحیحی از h/2π باشد، بنابراین اگر با تقریب مدار حرکت الکترون به دور هسته را دایرهای به شعاع r فرض کنیم، در این صورت nh/2π خواهد بود که در این رابطه v سرعت الکترون و m جرم آن است. همچنین با توجه به این که نیروی وارد شده از طرف هسته بر الکترون نیروی مرکزی است، لذا اگر بار هسته را برابر ze بگیریم که در آن z عدد اتمی است، مقدار نیروی وارد بر الکترون برابر ze2/r2 = mv2/r خواهد بود. از ترکیب این روابط میتوان مقدار انرژی الکترون در هر تراز اتمی را بدست آورد.
در این صورت انرژی از رابطه: E = 1/2mc2/(zα)2 بدست میآید که در این رابطه α مقدار ثابتی است که برابر α = 1/137 e2/ћc بوده و ثابت ساختار ریز نامیده میشود. مقدار n که در رابطه انرژی ظاهر شده است، عدد کوانتومی اصلی نامیده میشود. البته میتوان مقدار انرژی الکترون در هر تراز را از حل معادله شرودینگر محاسبه کرد. در این صورت نیز رابطه انرژی الکترون در هر تراز برحسب یک عدد کوانتومی که به عدد کوانتومی اصلی معروف است، مشخص میشود.
 |
عدد کوانتومی اندازه حرکت زاویهای مداری
نظریه اتم تک الکترونی بوهر عدد کوانتومی اصلی n را معرفی میکند که مقدار درست آن انرژی کل اتم را مشخص میکند. عدد کوانتومی n که یک عدد صحیح و مثبت است، بزرگی اندازه حرکت زاویهای الکترون به دور هسته را بر اساس اصل موضوع بوهر ، طبق رابطه L = nћ مشخص میکند. ћ عدد ثابتی است که بصورت نسبت ثابت پلانک بر عدد 2π تعریف میشود، اما از دیدگاه مکانیک موجی درست نیست که برای الکترون یک مسیر مشخص دایرهای یا شکل دیگری را در نظر بگیریم. (اصل عدم قطعیت مانع این کار است) و نیز از این دیدگاه قاعده بوهر در مورد کوانتش بزرگی اندازه حرکت زاویهای درست نیست.
بر خلاف نظریه کلاسیک ، مکانیک موجی نشان میدهد که بزرگی اندازه حرکت زاویهای مداری (L) یک دستگاه اتمی کوانتیده است و مقادیر ممکن آن میتواند از رابطه: L = (l(l + 1))1/2ћ بدست آید. در این رابطه l عدد صحیحی است که عدد کوانتومی اندازه حرکت زاویهای مداری نامیده میشود. برای مقدار مفروض از عدد کوانتومی اصلی n ، مقادیر ممکن l ، اعداد درست از صفر تا n - 1 خواهد بود. به عنوان مثال ، اگر n = 2 باشد، در این صورت l میتواند مقادیر (1,0) را اختیار کند.
در نمادگذاری ترازها هر مقدار از l با یک حرف مشخص میشود. در این نمادگذاری مقدار l = 0 با حرف S و l = 1 با حرف l = 2 ، P با حرف D و ... مشخص میشود. چون انرژی فقط برحسب عدد کوانتومی اصلی مشخص میشود، بنابراین در مورد تک الکترونی که تحت تأثیر یک نیروی کولنی از جانب هسته است و در تراز n = 3 قرار دارد، هر سه حالت l = 0 , 1 , 2 دارای انرژی یکسانی خواهند بود.
 |
اعداد کوانتومی مغناطیسی مداری
گفتیم که الکترون در اثر نیرویی که از طرف هسته بر آن وارد میشود، حول هسته میچرخد. چون الکترون یک ذره باردار است، بنابراین مدار الکترون را میتوان یک مدار مغناطیسی در نظر گرفت. برای این مدار مغناطیسی و در واقع برای الکترون میتوان یک گشتاور دو قطبی مغناطیسی تعریف نمود. این کمیت بر اساس اندازه حرکت زاویهای مداری الکترون تعریف میشود. یعنی از رابطه μ = eL/2m حاصل میشود که در آن μ گشتاور دو قطبی مغناطیسی است.
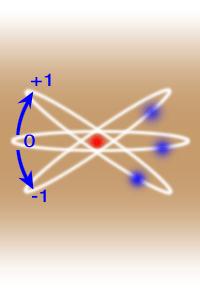
حال اگر یک میدان مغناطیسی خارجی اعمال شود، در این صورت میدان سعی میکند تا گشتاور دو قطبی مغناطیسی و به تبع آن L را در راستای میدان قرار دهد، اما در مکانیک موجی بردار اندازه حرکت زاویهای مداری L نمیتواند هر جهتی را نسبت به میدان مغناطیسی اختیار کند، بلکه محدود به جهتهای به خصوصی است که برای آن مؤلفه بردار اندازه حرکت زاویه مداری ، در راستای میدان مغناطیسی ، مضرب دستی از ћ باشد. بنابراین اگر جهت میدان مغناطیسی را در راستای محور z اختیار کنیم، در این صورت مؤلفه z بردار L از رابطه Lz = ml ћ حاصل میشود. در این رابطه ml عدد کوانتومی مغناطیسی مداری است. به ازای یک مقدار مفروض l ، m_l میتواند مقادیر زیر را اختیار کند:
{ml ={ l , l - 1 , l - 2 , … , 0 , … , - l
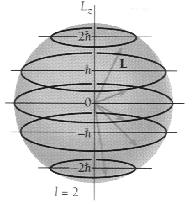 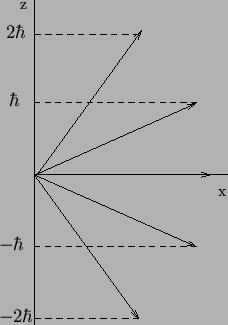 |
عدد کوانتومی مغناطیسی اسپینی
در نظریه کوانتومی سه ثابت فیزیک کلاسیک مربوط به حرکت ذرهای که تحت تأثیر جاذبه عکس مجذوری قرار دارد، کوانتیدهاند. این سه ثابت عبارتند از: انرژی ، بزرگی اندازه حرکت زاویهای مداری ، مؤلفه اندازه حرکت زاویهای مداری در یک جهت ثابت از فضا. در مکانیک کوانتومی به این ثابتهای حرکت اعداد کوانتومی n و l و ml نسبت داده میشوند، اما علاوه بر این سه عدد کوانتومی ، عدد کوانتومی دیگری به نام عدد کوانتومی اسپینی که به مفهوم اسپین الکترون مربوط است، معرفی میشود.
در سال 1925/1304 گود اسمیت و اوهلن یک اظهار داشتند که یک اندازه حرکت زاویهای ذاتی ، کاملا مستقل از اندازه حرکت زاویهای مداری ، به هر الکترون وابسته است. این اندازه حرکت ذاتی ، اسپین الکترون نامیده میشود. چون میتوان آن را با اندازه حرکت ذاتی که هر جسم گسترده بر اساس دوران یا اسپین حول مرکز جرم خود دارد، مانسته داشت. البته لازم به توضیح است که در مکانیک موجی تلقی الکترون به عنوان یک کره ساده با بار الکتریکی صحیح نیست، بلکه صرفا به خاطر مشخص کردن اندازه حرکت زاویهای اسپینی الکترون به کمک مدل قابل تجسم ، بهتر است که آن را به عنوان جسمی که در فضا دارای گسترش است و بطور پیوسته حول یک محور به دور خود میچرخد، فرض کنیم.
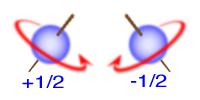 |
بنابراین اگر میدان مغناطیسی در راستای محور z فرض شود، در این صورت مؤلفه اندازه حرکت زاویهای اسپینی Lsz در جهت این میدان از رابطه Lsz = msћ حاصل خواهد شد. در این رابطه ms عدد کوانتومی مغناطیسی اسپینی نامیده میشود. از آنجا که الکترون از دسته فرمیونها میباشد، بنابراین دارای اسپین نیم فرد خواهد بود، لذا عدد کوانتومی ms فقط میتواند دو مقدار ممکن 2/1+ و 2/1- را اختیار کند.
کلمات کلیدی: کوانتوم
مقدمه
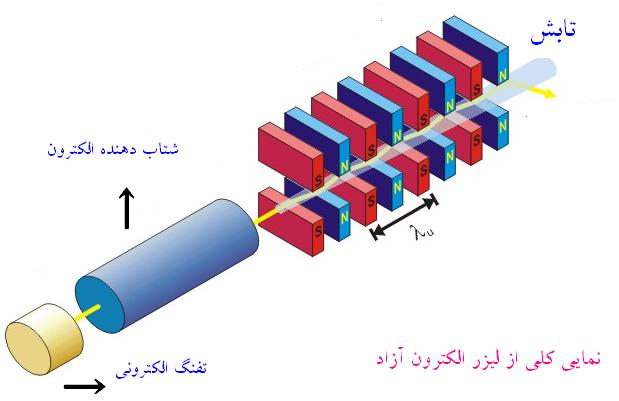 |
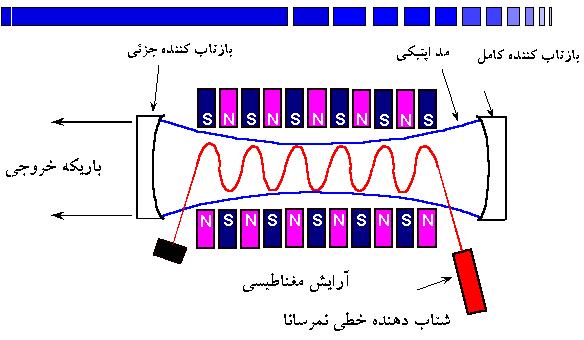
در لیزرهای رزینهای الکترونها مقید به یک اتم و یا یک مولکول هستند و یا در طول زنجیرهای از اتمها که مولکول دو قطبی را تشکیل میدهند، آزادی حرکت دارند. نیز در لیزرهای نیم رسانا الکترونها میتواند که در تمام حجم بلور حرکت کنند. ولی در لیزر الکترون آزاد ، که یکی از جدیدترین و جالبترین انواع لیزرهاست، الکترونها بیشتر از موارد فوق الذکر آزادی حرکت دارند.
در لیزر الکترون آزاد الکترونها آزادانه در یک میدان مغناطیسی متناوب حرکت میکنند و در اثر برهمکنش میدان الکترومغناطیسی با الکترونهایی که در این ساختار تناوبی در حرکتند، فرآیند گسیل القایی رخ میدهد. از نظر تاریخی ، لیزر الکترون آزاد اولین بار در سال 1951 بوسیله Mets پیشنهاد شد. این لیزر قادر به کار در ناحیه طیفی مرئی و ماوراء بنفش هستند، ولی تا کنون این لیزرها تنها در طول موج λ = 3/4µm عمل کرده است.
سینماتیک اندرکنش الکترون آزاد- فوتون
لیزرهای الکترون آزاد ، علت تشعشع انرژی الکترومغناطیسی ، شتاب الکترونها در میدان متناوب است. نمونه مشابه برای چنین تشعشعی ، تشعشع سینکروترون الکترونهایی است که در یک میدان مغناطیسی حرکت دایرهای انجام میدهند ولی این تشعشع طیف وسیعی را میپوشاند، لذا برای نوسان لیزری مناسب نیست. در لیزر الکترون آزاد ، الکترونها مجبورند در جهت عرضی (x یا y) حرکت موجی انجام دهند، در حالیکه با سرعتهای نسبیتی در جهت محور اصلی (z) حرکت میکنند.
 |
توان ExVx که از باریکه الکترون به موج الکترومغناطیسی جاری میشود، پیوسته است (این توان حادی شده ممکن است منفی باشد). فرکانسهای گذار فرکانسهایی هستند که طی آن سرعت الکترون تغییر جهت میدهد. الکترون آزاد ، انرژی E1 از میدان الکتریکی یک فوتون با انرژی Eph جذب کرده و یا به آن یک فوتون میدهد و با انرژی E2 خاتمه مییابد.
چون الکترونها حرکت نسبیتی دارند لذا انرژی آنها نیز باید از روابط نسبیتی محاسبه شود. اما مشاهده میکنیم که تغییر در انرژی Ee∆ یک الکترون ، ایجاد یک گذار از مختوم P1 به P2 میکند که کوچکتر از انرژی (P1 - P2) فوتون با مختوم (P1 - P2) میباشد. این نتیجه در سه بعد نیز صادق است. یکی از راه حلهای این مسئله میانجیگری در اندرکنش بین الکترون و باریکه نور (فوتونها) بوسیله انتقال پریودیک فضایی است که با مضاربی از 2π/L جذب میکند (L پریود است)، اختلال میتواند بر فوتون ، الکترون و یا هر دو اثر کند.
برای مشاهده نحوه عمل ، فرض میکنیم در تیوبهای موج رونده میکروویو ، جائیکه میدان الکترومغناطیسی در یک ساختار پریودیک منتشر میشود، به میدان یک حرکت پریودیک اضافی وارد میشود. در مورد یک لیزر الکترون آزاد ، این حرکت الکترون است که بطور پریودیکی با بکار بردن یک میدان مغناطیسی بطور فضایی پریودیکی مدوله میشود. البته میتوان میدان الکترومغناطیسی را بطور فضایی مدوله کرد، این کار با بکار بردن یک موجی که بطور فضایی پریودیکی است، عملی میباشد.
هرگاه در تیوبهای موج رونده و شتاب دهندههای خطی ذرات باردار ، به نقطه نظر کلاسیکی برگردیم: یک الکترون را در نظر میگیریم که با سرعت V در حرکت است و با یک میدان الکترومغناطیسی رونده که میدانهای مغناطیسی و الکتریکی آن به ترتیب بصورت (E(r,t)B(r,t است، اندرکنش میکند.
شرط همزمانی (The synchrcnism crndition)
برای اینکه یک تبادل انرژی بین الکترون (با انرژی γmc2) و یک میدان E صورت میگیرد، لازم است که سرعت الکترون (v) در امتداد E ، مؤلفه غیر صفر داشته باشد. (γ ضریب تبدیل جرم نسبیتی است) در مورد موج الکترومغناطیسی تخت که در جهت z منتشر میشود Ez = 0 بوده و Ex ≠ 0 است. برای اینکه بایستی بررسی الکترون یک مؤلفه عرضی Vx داشته باشیم، چون Vz < c است، الکترون نسبت به موج عقب میافتد و بایستی تغییر علامت دهد (جهت سرعت تغییر میکند)، لذا تبادل خالص انرژی بین الکترون و باریکه متوسط گیری میشود.
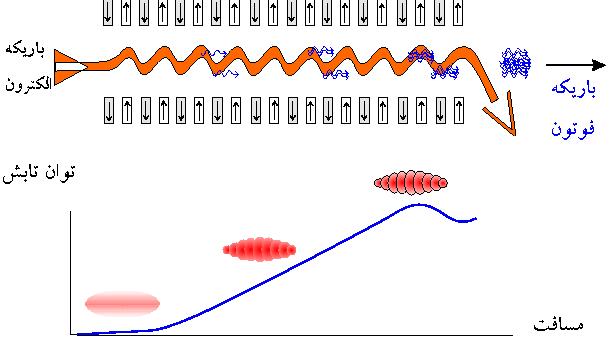 |
یک راه حل آشکار این مسئله ودار کردن الکترون به تغییر سرعتش میباشد. بطوری که در یک جهت با میدان عرضی حرکت میکند. این کار با بکار بردن یک میدان مغناطیسی عرضی پریودیکی فضایی (با پریود 0λ) در حضور یک موج الکترومغناطیسی تخت با طول موج λ بیان میشود. بردار سرعت الکترون در z = 0 با میدان روبرو شده و دارای یک سرعت عرضی موازی جهت میدان (Vx||Ex) میباشد. بطوری که VxEx>0 است. یک الکترون مشابه در دو نقطه اضافی دیگر نشان داده شدهاند. بخشی از یک میدان الکتریکی که در ابتدا در نقطه z = 0 با الکترون روبرو شده ، در نقطه Vx 0 است، ولی میدان الکترومغناطیسی سریعتر و جلوتر از الکترون حرکت میکند بطوری که Ex < 0 و ExVx > 0 است.
در نقطه z = λ0 ، Vx > 0 است و Ex > 0 است لذا ExVx>0 میباشد. بنابراین در هر نقطه ExVx> 0 است و الکترون بطور پیوسته قرمز شده و به میدان اپتیکی انرژی میدهد. شرط تشدید P1 - P2 = ±t.k میباشد.
نشر خود به خودی و بهره در FEL
وقتی که الکترون در میدان مغناطیسی wigglel حرکت شتابدار انجام میدهد (و این شتاب پریودیک و عرضی میباشد) و از آن یک تشعشع خودبخودی بوجود میآید، بطوری که طیف حاصل از این تشعشع از روابط مشابه توری پیروی میکند. (پریودهای میدان مغناطیسی برای الکترون به مثابه توری میباشد). الکترون شتابدار موج الکترومغناطیسی تشعشع میکند و این تشعشع در یک ساختار پریودیک صورت میگیرد. بهره به عنوان اختلاف بین آهنگ نشر و جذب تحریکی بوسیله الکترونهای تشعشعی میباشد.
مزایا وکاربردهای FEL
-
یکی از مزیتهای FEL نسبت به لیزرهای اتمی این است که در FEL با افزایش طول اندرکنش L ، بهره الزاما افزایش پیدا نمیکند و ممکن است بهره از بین رفته و حتی منفی شود و خود L افزایش مییابد، فرکانس برای ماکزیمم بهره به مقدار تشدید خود نزدیک میشود.
-
در نوسانگرهای FEL تشعشع از افت و خیز چگالی باریکه الکترونی و یا از نشر خودبخودی آغاز میشود و هنگامی که توان تبدیلی از باریکه الکترونی بتوان تشعشعی از اتلافات تشعشع در مشدد زیاد باشد عمل لیزر صورت میگیرد. مزیت اصلی FEL به لیزرهای کوانتومی قابلیت تنظیم تشعشع آن میباشد. در لیزرهای کوانتومی طول موج لیزر بوسیله انرژی گذارهای بین ترازهای کوانتومی اتمها یا مولکولها در ماده فعال مشخص میشود و علیرغم تنوع و تعداد مواد فعال لیزری تعداد ترازهای کوانتومی محدود است (محدود به معنی متناهی) ولی در FEL ها طول موج لیزر بوسیله پارامترهای باریکه الکترونی و ساختار الکترودینامیکی آنها مشخص میشود (دیوارهای موجی ، آینههای مشدد و ...) نیز با مشخصههای میدانهای الکتریکی و مغناطیسی در ناحیه اندرکنش.
-
تشعشع FEL میتواند بر یک نقطه که سایز آن با پدیدههای پراش مشخص میشود، متمرکز گردد.
-
تقویت نور در FEL ها در خلأ صورت میگیرد، لذا اثرات ماده فعال روی نور وجود ندارد و پراش نیز کم است. لذا این لیزر برای طی مسیر طولانی و توانهایی بالا مناسب است، ولی در لیزرهای معمولی بخاطر پراکندگی ماده فعال توان خروجی کم است، ولی مشکل عمده FEL ها تکنیک شتاب دهنده الکترونی است.
-
بهره FEL ها بالای 100% است، ولی محدودیتهای موجود (نه از نظر فیزیکی) باعث شده که رکورد بهره از 34% تجاوز نکند.
از این لیزرها در علم و صنعت ، مانند فعل و انفعالات مواد میکرو لیتوگرافی ، جداسازی ایزوتوپها ، کاربردهای شیمیایی ، گرمایش پلاسما و ... استفاده میشود
کلمات کلیدی: اپتیک
| نیروی جانب مرکز ، نیرویی است که به جسمی که به یک انتهای ریسمانی بسته شده است و حول نقطهای در یک مسیر دایروی حرکت میکند، وارد میشود و جهت آن همواره به سمت مرکز دایره است. به عبارتی در حرکت دایروی یکنواخت برآیند نیروهای وارد بر جسم که در راستای شعاع بسوی مرکز است، همان نیروی جانب مرکز میباشد. |
دید کلی
در مثال ریسمان نیرویی از طرف ریسمان بر وزنه وارد میشود که اگر از سنگینی وزنه و اثر مقاومت هوا صرفنظر کنیم، در این صورت این نیرو ، تنها نیرویی خواهد بود که سبب تغییر جهت سرعت میگردد و به آن شتاب میدهد. اگر چنانچه ریسمان پاره شود، در این صورت وزنه در راستای مماس بر مسیر حرکت با همان سرعتی که قبل از پاره شدن طناب داشت، به خارج پرتاب میشود. اما تا زمانی که ریسمان پاره نشده است، نیروی کشش ریسمان وزنه را مجبور میکند که بر یک مسیر دایرهای حرکت کند. چون جهت این نیرو همواره متوجه مرکز دایره است، برای همین است که این نیرو را نیروی جانب مرکز نام نهادهاند.
تاریخچه
جهت نیرویی که این حرکت را ایجاد میکند باید بسوی مرکز باشد، اگر چرخیدن شیء را تصور کنیم که به ریسمانی با طول L متصل است، بوضوح میبینیم که جهت صحیح برای نیرو باید همین جهت باشد، ریسمان تحت تأثیر کشش ثابتی قرار دارد. همین کشش است که شیء را در مسیر دایرهای نگه میدارد. از تجربه روزمره میدانیم که شیء متحرک به طرف خارج از دستی کشیده میشود که ریسمان را نگه داشته است. از قانون سوم نیوتن نیرویی که دست از طریق ریسمان بر شیء وارد میآورد باید نیروی کششی برابر بسوی دست باشد، این نیرو که جهتش به طرف داخل است، نیروی جانب مرکز نامیده میشود.
اندازه نیروی جانب مرکز
نیروی جانب مرکز ، در حرکت یکنواخت بر مسیر دایرهای عبارتست از نیرویی با اندازه ثابت که بطور مداوم عمود بر مسیر حرکت ، بر جسم اثر میکند و سبب میشود که جسم با سرعت ثابت روی دایره حرکت کند. از طرف دیگر ، چون بر اساس قانون دوم نیوتن نیرو را برحسب حاصل ضرب شتاب در جرم ذره تعریف کردهایم، لذا اگر جرم جسم را با m نشان دهیم، در این صورت چون شتاب جانب مرکز را به صورت
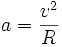 یا
یا 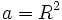 تعریف کردهایم، لذا نیروی جانب مرکز از رابطه زیر محاسبه خواهد شد:
تعریف کردهایم، لذا نیروی جانب مرکز از رابطه زیر محاسبه خواهد شد:
بدست آوردن رابطه نیروی جانب مرکز
محاسبه شتاب جانب مرکز
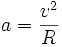 حاصل خواهد شد که در آن a شتاب جانب مرکز است. بدیهی است که جهت این شتاب نیز مانند نیروی جانب مرکز در جهت مرکز دایره مسیر حرکت خواهد بود.
حاصل خواهد شد که در آن a شتاب جانب مرکز است. بدیهی است که جهت این شتاب نیز مانند نیروی جانب مرکز در جهت مرکز دایره مسیر حرکت خواهد بود.اگر چنانچه جابجایی ذره را بر حسب زاویهای که بردار شعاعی طی میکند، بیان کنیم، در این صورت به جای جابجایی خطی جابجایی زاویهای خواهیم داشت. لذا تغییرات جابجایی زاویهای نسبت به زمان را به صورت سرعت زاویهای تعریف میکنیم. بنابراین میتوان شتاب جانب مرکز را برحسب سرعت زاویهای بیان کرد. یعنی اگر ω سرعت زاویهای باشد، در این صورت شتاب جانب مرکز از رابطه زیر حاصل میشود:
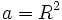
اکنون نیروی جانب مرکز با استفاده از قانون دوم نیوتن بدست میآید: Fc= mac = mv²/r = mrw²
مواردی که در آنها نیروی جانب مرکز مشهور است.
آونگ مخروطی
حرکت در پیچ جاده
حرکت ماهواره دور زمین
حرکت الکترون در مدار خود
نیروی گریز از مرکز
برای اینکه واقعا بدانبم نیروی گریز از مرکز یک نیروی مجازی است، فرض کنید که ناظری در روی مرکز دایره ایستاده است و همراه این محور با سرعت زاویهای ω میچرخد. این ناظر همواره وزنه را ساکن میبیند، چون نیروی کشش نخ که متوجه مرکز است، برای این ناظر نیز وجود دارد. این ناظر میتواند اندازه این نیرو را بسنجد. برای توجیه حالت سکون نیز ، نیرویی مساوی با نیروی جانب مرکز و در خلاف جهت آن به نام نیروی گریز از مرکز در نظر میگیرند.
اما از دید ناظری که در روی زمین ساکن است و این حرکت را مشاهده میکند، نیروی گریز از مرکز مفهومی ندارد. چون در این حالت جسم ، در اثر ضربهای که بر آن وارد میشود و سرعتی که در اثر ضربه پیدا میکند، بر اساس قانون اول نیوتن میخواهد که در امتداد خط راست حرکت کند، ولی نیروی جانب مرکز آن را مجبور میکند که بر روی محیط دایره حرکت کند.
کلمات کلیدی: فیزیک نوین
نگاه کلی
یک مولد یا ژنراتور اشعه ایکس وسیلهای است که انرژی الکتریکی را جهت لامپ اشعه ایکس فراهم مینماید. در واقع این وسیله انرژی مکانیکی را به انرژی الکتریکی تبدیل مینماید. این ژنراتور با یک منبع انرژی الکتریکی شروع میشود و سپس این انرژی را به نحوی تغییر میدهد تا نیاز لامپ اشعه ایکس را مرتفع سازد. لامپ به دو منظور به انرژی الکتریکی نیازمند است. ابتدا برای ملتهب نمودن فیلمان (کاتد) و تابش الکترون از آن ، سپس شتاب دادن به این الکترونها از کاتد به سمت آند. ژنراتور اشعه ایکس برای هر کدام از این اعمال دارای یک مدار خاص میباشد که به ترتیب مدار فیلمان و مدار ولتاژ قوی نامیده میشوند.
 |
قسمتهای مختلف ژنراتور اشعه ایکس
صفحه کنترل ژنراتور
صفحه کنترل شامل یک کلید اصلی جهت روشن نمودن دستگاه ، دو عدد وسیله اندازه گیری که میزان حقیقی MA وKVP را در خلال تولید اشعه ایکس اندازه گیری مینماید، است.
مجموعه مبدل
دومین جز ژنراتور اشعه ایکس یعنی مجموعه مبدلها یک جعبه فلزی با اتصال زمین پر شده از روغن است. این جعبه شامل یک مبدل کاهنده برای مدار فیلمان و یک مبدل افزاینده برای مدار ولتاژ قوی میباشد. بنابراین یک مبدل وسیلهای است که ولتاژ را در یک مدار افزایش یا کاهش میدهد. این قسمت شامل دو سیم پیچ میباشد که به دو طرف یک حلقه آهنی پیچیده شده است. هنگامیکه جریان از میان سیم پیچ اول عبور مینماید، یک میدان مغناطیسی در یک حلقه آهنی ایجاد شده و موجب القای یک جریان در سیم پیچ ثانویه میگردد. اما این نکته مهم است که یک جریان فقط هنگامی در مدار ثانویه عبور مینماید که میدان مغناطیسی افزایش و کاهش یابد.
هنگامیکه میدان مغناطیسی در حالت پایدار است، هیچ جریانی از مدار عبور نخواهد کرد. به این علت استفاده از یک جریان ثابت مستقیم (مانند جریان یک باتری) در سیم پیچ اولیه قادر به ایجاد یک جریان مداوم در سیم پیچ ثانویه نمیباشد. بکار گیری جریان متناوب در مبدلها به علت آن است که این نوع جریان بوسیله یک اختلاف پتانسیل تولید شده و بطور مداوم اندازه و به صورت متناوب جهت آن تغییر مینماید. یعنی مهمترین مشخصه جریان متناوب تغییر پیوسته ولتاژ آن میباشد که بدین ترتیب یک میدان مغناطیسی که دائما در حال تغییر است، ایجاد مینماید.
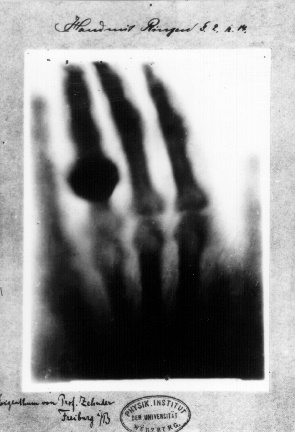 |
|
|
انواع مبدل
یک مبدل با تعداد دورهای بیشتر در سیم پیچ ثانویه نسبت به سیم پیچ اولیه موجب افزایش ولتاژ میگردد که بدین ترتیب آن را یک مبدل افزاینده مینامند. یک مبدل با دورههای کمتر در سیم پیچ ثانویه موجب پایین آوردن ولتاژ شده و به نام مبدل کاهنده نامیده میشود.
اتو ترانسفورماتور و وظایف آن
ولتاژ تحویلی به اتاق رادیوگرافی از طریق یک اتو ترانسفورماتور به ژنراتور اشعه ایکس متصل میگردد. اتو ترانسفورماتور دارای چندین وظیفه است که به شرح زیر میباشد.
-
فراهم آوردن ولتاژ لازم برای مدار فیلمان.
-
فراهم آوردن ولتاژ لازم برای مدار اولیه مبدل ولتاژ قوی.
-
فراهم آوردن یک محل مناسب برای قرار دادن وسیله نمایش KVP که نشانگر ولتاژ اعمال شده به دو سر لامپ است.
یک اتو ترانسفورماتور شامل یک سیم پیچ منفرد بر روی یک هسته آهنی لایه لایه بوده و بر اساس اصل خود القایی کار میکند. اعمال یک جریان متناوب ، یک میدان مغناطیسی در اطراف هسته القا خواهد نمود. که این میدان با تمام دورهایی که سیم پیچ را تشکیل میدهد، در ارتباط است و با انتخاب نقطه اتصال مناسب میتوان تعداد دورهای لازم برای فراهم کردن ولتاژ مورد نیاز سایر اجزای ژنراتور اشعه ایکس را فراهم آورد. اتو ترانسفورماتور در یک محدوده بسیار کوچک میتواند عمل یک مبدل افزاینده یا کاهنده را انجام دهد.
کلمات کلیدی: هسته ای



.GIF)



