دیدکلی

می‌دانیم که تمام قوانین حرکت ، چه قوانین نیوتن و چه قوانین ماکسول برای میدانهای الکترومغناطیسی متحرک ، باید با یک چارچوب مرجع همراه باشند. در عین حال ، یک فرآیند فیزیکی نباید به چارچوبی که ناظر برای مشاهده آن انتخاب کرده است، وابسته باشد. پس قوانین فیزیکی را باید به صورتی نوشت که در سیستم‌های مختصات مختلف شکلشان حفظ شود. بنابراین تبدیلی که با اعمال آن فرم ریاضی قانون فیزیکی در چارچوب‌های مختلف لخت ، ثابت بماند، اهمیت اساسی دارد. تبدیل که در زمان نیوتن رواج داشت، تبدیلات گالیله بود:

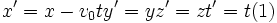
این تبدیل در اینجا برای دو چارچوب لخت ، پریم‌دار و بدون پریم ، که نسبت به هم با سرعت 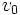در جهت x حرکت می‌کنند، بیان شده است.
تاریخچه

اینکه قوانین نیوتن تحت تبدیلات گالیله ناوردا هستند، مطلبی شناخته شده بود. با وجود این نیوتن معتقد بود که قوانینش به یک چارچوب مرجع مطلق وابسته است. البته این فکر کاملا متافیزیکی است، چون خود او اصل نسبیت در مکانیک را وضع کرده بود که بر طبق آن ، تعیین حرکت مستقیم الخط یک جسم متحرک ، یا یک چارچوب مرجع ، نسبت به این سیستم مطلق غیر مطلق ناممکن است.

برای مثال شتاب و نیرو در این دو چارچوب مرجع مشابه‌اند، چون طبق روابط (1) داریم: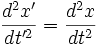



پس F"=ma تحت تبدیلات گالیله به صورت F=ma در می‌آید، یعنی تحت این تبدیلات ناوردا است. دلیل این ناوردایی عدم ظهور سرعت در معادله حرکت است.

معادلات ماکسول و تبدیلات گالیله

اگر تبدیلات گالیله را در مورد معادلات ماکسول اعمال کنیم، شکل معادلات در سیستم‌های مختصات مختلف فرق خواهد کرد، چون سرعت انتشار امواج الکترومغناطیسی در معادلات ظاهر می‌شود، لذا وقتی این سرعت به صورت برداری جمع شود، در سیستم‌های مختصات مختلفی که نسبت به هم حرکت می‌کنند، مقادیر مختلفی خواهد داشت. تفاوت سرعت چند مفهوم ضمنی دارد، اول اینکه تشخیص چارچوب مرجع مطلق به روش الکترومغناطیسی یا نوری ممکن خواهد بود. در آن زمان فرض می‌شد که نور برای انتشار نیاز به محیط خاصی دارد، و این محیط اتر نامیده می‌شد.

این حقیقت که معادلات ماکسول تحت تبدیلات گالیله تغییر می‌کنند، مستلزم این بود که سیستم مرجعی وجود داشته و اتر نسبت به آن ساکن باشد. سرعت نور در این چارچوب مطلقا ساکن ، C است و احتمالا در یک چارچوب مرجع دیگر C نخواهد بود. اینکه سرعت نور در دو سیستم مختصات مختلف تحت تبدیلات گالیله متفاوت است، از رابطه (1) پیداست. اگر سرعت نور در یک چهارچوب S (بدون پریم) dx/dt باشد، در چهارچوب "S که نسبت به S با سرعت 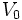حرکت می‌کند، به صورت 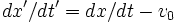خواهد بود.

ثابت بودن سرعت نور

با این حال آزمایش فیزو ، آزمایش مایکلسون - مورلی و آزمایشهای متعدد دیگری که هدفشان بررسی دقت معادلات ماکسول در چارچوبهای مرجع متحرک بود، نشان داد که بی‌شک سرعت نور در تمام جهتها و در تمام سیستم‌های مرجع متحرک یکسان است. بنابر این نتیجه می‌گیریم که معادلات ماکسول باید در تمام مختصات لخت شکل خود را حفظ کند.

تبدیلات لورنتس

لورنتس که سعی می‌کرد تبدیلات گالیله را بهبود بخشد، تبدیل جدیدی یافت که تحت آن معادلات ماکسول در سیستم‌های مختصات مختلفی که نسبت به هم حرکت دارند، تغییر نمی‌کرد و به این ترتیب اساس نسبیت خاص بنا نهاده شد. این تبدیل اکنون تبدیلات لورنتس نامیده می‌شود: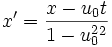





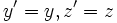
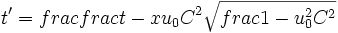
کمی‌ بعد پوانکاره نشان داد که تمام معادلات الکترودینامیک تحت تبدیلات لورنتس شکل خود را حفظ می‌کند. یک امتحان ساده نشان می‌دهد که در تبدیلات لورنتس 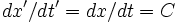. انیشتین در سال 1905 این فکرها را تعمیم داد و به صورت نسبیت خاص فعلی در آورد. او نشان داد که با پذیرفتن نسبیت نیوتن ، می‌توان تبدیلات لورنتس را بدست آورد. انیشتین فرض کرد که سرعت نور یک ثابت جهانی و مستقل از حرکت چشمه آن است.

گرچه ریشه نسبیت خاص در الکترومغناطیس بود، ولی روش انیشتین وابستگی صریحی به الکترودینامیک نداشت. چون معادلات ماکسول تنها یکی از قوانین فیزیکی است که اصول نسبیت خاص آن را در بر می‌گیردف بنابر این نسبیت خاص نتایج وسیعی داشت. به این ترتیب مفهوم اتر از بین رفت.

مفهوم زمان در نسبیت خاص

بر اساس اصل دوم نسبیت خاص مفهوم کلاسیکی زمان ، به عنوان یک متغیر مستقل از دستگاه مختصات و حرکت نسبی از بین رفت و مفهوم پیچیده و مشکل فضا_زمان جانشین آن شد. در همزمانی وقایع باید تجدید نظر کرد. وقایعی که در یک سیستم مختصات همزمان هستند، لزوما در سیستم دیگری که نسبت به اولی حرکت دارد، همزمان نیستند. این ایده‌ها چنان تکان دهنده بود که خیلی‌ها به تندی با آن مخالفت کردند و شاید هنوز هم می‌کنند. برای ارائه فرضیه‌ای که به اصل موضوع دوم محتاج نباشد، کوشش‌های هوشمندانه بسیاری شد. تاکنون آزمایشهای مختلف و متعددی پیش‌بینی‌های نسبیت خاص را تصدیق کرده‌‌اند، طوری که تنها می‌توان فرضیه‌های سازگار با نسبیت خاص را در نظر گرفت.

قوانین کلاسیک و تبدیلات لورنتس

قوانین کلاسیک الکترودینامیک که تحت تبدیلات گالیله ناوردا هستند، با تبدیلات لورنتس نیز ناوردا می‌مانند. ولی معادلات مکانیک کلاسیک که تحت تبدیلات گالیله ناوردا بودند، اکنون با تبدیلات لورنتس ناوردا نیستند، یعنی یا باید آنها را دور ریخت و یا با معادلات نسبیتی جایگزین کرد. در معادلات نسبیتی جرم یک جسم m که با سرعت v حرکت می‌کند، با جرم آن در حالت سکون ، 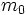، به صورت زیر مرتبط است:

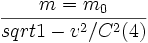
خوشبختانه این تنها تصحیح لازم برای قوانین مکانیک است. در سرعتهای کم که 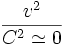معادلات نسبیتی به قوانین حرکت نیوتن تبدیل می‌شوند. لزوم تصحیح نسبیتی در قوانین حرکت خیلی زود با آزمایش تائید شد. برای مثال الکترونها را می‌توان در یک شتابدهنده شتاب داد و سرعتشان را نزدیک به سرعت نور رساند، طوری که جرمشان چند هزار برابر شود.

انرژی سکون

با بسط رابطه (4) یک جمله 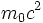نتیجه می‌شود که انیشتین ، لویس و دیگران آن را انرژی سکون 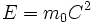تشخیص دادند. پیش‌بینی این انرژی بسیار زیاد جرم ، در آزمایش‌های شکافت (فیزیون) و ابزارهای هسته‌ای تایید شد.

شاید بهترین و ساده‌ترین مثال نشان دهنده 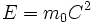هنگامی ‌باشد که یک الکترون و پاد الکترون (پوزیترون) ، که جرم هر دو 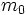است، ترکیب می‌شوند. این دو همدیگر را نابود می‌کنند و دو اشعه گاما بوجود می‌آید. انرژی اشعه گاما با انرژی سکون دو ذره قبل از برخورد ، 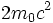، برابر است.

تبدیلات گالیله

دید کلی

در برسی حرکت هر ذره باید یک چارچوب مرجع تعین کنیم که این چارچوب به عنوان ناظر در فیزیک تعبیر می‌شود. بعد از تعیین چارچوب مرجع به راحتی می‌توانیم حرکت را مورد برسی قرار دهیم. البته لازم به ذکر است که در مورد هر حرکت ، چارچوب خاصی متناسب با نوع حرکت باید بکار ببریم. این مسئله نه تنها در مورد حرکت بلکه در مورد تمام رویدادها و پدیده‌های فیزیکی مطرح است.

به عنوان مثال برای اینکه بتوانیم در الکترو مغناطیس مقدار نیروی وارد بر یک جسم باردار را محاسبه کنیم، ابتدا باید یک چارچوب متناسب با سیستم تعریف کرده ، سپس پدیده را مورد برسی قرار دهیم. حال سوال این است که اگر این چارچوب مرجع تغییر بکند (به عنوان مثال اگر چارچوب مرجع منتقل شود) ، در این صورت چه تغییری در برسی حاصل خواهد شد. این مسئله بوسیله قواعد تبدیل بیان می‌شود.

تعریف

معادلاتی که در فیزیک کلاسیک مختصات فضا و زمان دو دستگاه مختصات را ، که با سرعت ثابت نسبت به یکدیگر حرکت می‌کنند به هم مربوط می‌سازند، تبدیلات گالیله یا نیوتنی نامیده می‌شوند. هر ناظر با مشخص کردن مکان و زمان یک پدیده فیزیکی ، مانند یک بمب کوچک ، هر رویدادی را می‌تواند توصیف کند. اگر مختصات فضایی و زمانی یک رویداد ، از نظر ناظر S₁ بصورت:

لازم به ذکر است که تبدیلات سرعت و شتاب نیز با مشتق گیری از روابط فوق حاصل می‌شود.
هموردایی مکانیک کلاسیک در تبدیلات گالیله

در فیزیک به عنوان یک اصل پذیرفته می‌شود که ، قوانین فیزیک در تمام دستگاههای لخت یکسان ، یا هموردا ، هستند. یعنی شکل ریاضی یک قانون فیزیکی یکسان باقی می‌ماند. به عبارت دیگر می‌توان گفت که باید قوانین فیزیک تحت تبدیلات گالیله یکسان باقی بمانند. از جمله قوانین فیزیکی که تحت این تبدیلات فرم ریاضی خود را حذف می‌کنند، قوانین بقای اندازه حرکت خطی و قانون بقای انرژی است. همچنین قانون دوم نیوتن نیز که قانون بقای اندازه حرکت خطی از آن نتیجه می‌شود، فرم ریاضی خود را حفظ می‌کند.

به عبارت دیگر می‌توان گفت که تبدیلات گالیله و مکانیک کلاسیک مستلزم آن هستند که سه کمیت اساسی در آزمایشهای فیزیکی ، یعنی طول ، زمان و جرم همگی از حرکت نسبی هر ناظری مستقل باشد. البته فیزیک نسبیت انیشتن در این عقیده تجدید نظر می‌کند. و بجای طول ، زمان ، جرم و انرژی، دو قانون بقای جدید بوجود می‌آورد. یعنی طول و زمان را باهم ادغام کرده و یک کمیت ناوردا در فضای چهار بعدی بوجود می‌آورد و نیز قانون بقای جرم و انرژی را هم یکجا در رابطه هم ارزی جرم و انرژی بیان می‌کند.

الکترو مغناطیس و تبدیلات گالیله

در اوایل توسعه نظریه موجی نور این سوال مطرح شد که آیا امواج الکترومغناطیسی در محیط واقعی منتشر می‌شوند یا در اتر. اگر انتشار در اتر انجام می‌شد، در آن صورت فرض بر این بود که محور‌های مختصات واقع در آن محیط باید چارچوب مشخصی را تشکیل دهند، بطوری که همه ناظرها نسبت به آن ساکن یا در حرکت نسبی باشند. حال به خوبی می‌دانیم که همه کوششهای تجربی برای کشف وجود یک محیط ساکن که در آن امواج الکترومغناطیسی منتشر شوند با شکست مواجه شد.

لذا نتیجه می‌گیریم که از نظر هر ناظر لخت ، نور در فضا با تندی استاندارد c ، بدون توجه به حالت یکنواخت او نسبت به هر چارچوب مختصات دیگر بطور همسانگرد منتشر می‌شود. ناوردایی سرعت نور بر این شرط فیزیکی دلالت دارد که معادله‌های الکترومغناطیس باید در اثر تبدیل مختصات هر چارچوب مرجع ، در حرکت یکنواخت نسبت به چارچوب اصلی به طریقی تبدیل شوند، که صورت اصلی‌شان حفظ شود. اما معادله موج که از معادلات ماکسول حاصل می‌شود ، تحت تبدیلات گالیله شکل ریاضی خود را حفظ نمی‌کند. بنابراین ، بجای استفاده از تبدیلات گالیله از تبدیلات لورنتس که یک جایگزین قوی برای تبدیلات گالیله است، استفاده می‌کنیم.

دلایل ضعف تبدیلات گالیله

• براساس تبدیلات گالیله جرم ، زمان و طول همواره مستقل از حرکت نسبی ناظر ناوردا می‌باشند. در صورتی که می‌دانیم در سرعتهای نزدیک به سرعت نور در اثر حرکت ، انقباض طولی و اتساع زمان خواهیم داشت. جرم ذره نیز با جرم در حالت سکون آن متفاوت خواهد بود.
  
  
• بر اساس تبدیلات گالیله صورت و فرم معادلات ماکسول هنگام تبدیل مختصات تغییر می‌کنند.
  
  
• بر اساس تبدیلات گالیله سرعت نور نمی‌تواند مستقل از حرکت نسبی ناظرها باشد. در صورتی که می‌دانیم بر اساس اصل موضوع نسبیت خاص ، سرعت نور باید مستقل از حرکت نسبی ناظرها مقداری ثابت باشد.

نتیجه‌گیری نهایی

بر اساس دلایل فوق می‌توان چنین نتیجه گرفت که ، تبدیلات گالیله نمی‌توانند یک تبدیل جامع و کامل باشد. لذا باید از یک تبدیل جامعتر که قادر به توضیح تمام قوانین فیزیک باشد، استفاده کنیم. چنین تبدیلی ، تبدیلات لورنتس می‌باشد. این تبدیل بر اساس دو اصل ، ناوردایی سرعت نور و اصل هم ارزی ایجاد شده است.

تبدیلات لورنتس (Lorentz transformations)

اطلاعات اولیه

در اواخر قرن نوزدهم ، بعد از اینکه نظریه الکترومغناطیس کلاسیک به صورت کنونی اش توسعه یافت، نیاز به یک نظریه نسبیت رضایتبخش در فیزیک احساس شد. در آن زمان آشکار شد که مشاهدات تجربی انتشار نور در ارتباط با اثر‌های حرکت ناظر نسبت به محیطی که فرض می‌شد نور در آن حرکت می‌کند تناقض‌هایی با عقاید رایج آن زمان دارد. برای داشتن توصیفی از حرکت نور که با تجربه سازگار باشد، لازم شد قانون تبدیل پیشنهادی لورنتس که مختصات چارچوبهای دارای حرکت نسبی یکنواخت را به هم مربوط می‌سازد، پذیرفته شود. این قانون تبدیل ، به نام تبدیلات لورنتس معروف است.

تعیین تبدیلات لورنتس

به طور خلاصه می‌توان گفت که ، تبدیل مختصات در چارچوبهای لخت که از نظر نسبیت صحیح باشد، توسط دو اصل حاکم زیر تعیین می‌شود:

• در تمام چارچوبهای لخت ، نور به طور همسانگرد با سرعت ثابت c میسر را می‌پیماید.
• تمام چارچوبهای مرجع لخت در بیان قوانین فیزیکی به طور یکسان معتبر هستند.

با اعمال دو اصل فوق می‌توان تبدیلات لورنتس را به روش مقدماتی بدست آورد. بنابراین اگر دو چارچوب مختصه متعامده E₁ و E₂ ، را که با سرعت نسبی ثابت U در امتداد محور ایکس (X) شان حرکت می‌کنند در نظر بگیریم. در اینصورت هرگاه مختصات یک رویداد در چارچوب اول را با X₁y₁ z₁ t₁ و مختصات همان رویداد در چارچوب دوم را با x₂ y₂ z₂ t₂ نشان دهیم، در اینصورت تبدیل لورنتس که بیانگر روابط تبدیل بین مختصات رویداد مورد نظر هنگام رفتن از یک چارچوب به چارچوب دیگر است، به صورت زیر خواهد بود.

Z₂=z₁

T₂=(t₁+Vx/c²)/1-(v/c)^21/2

اصل توافق

• ملاحظه کردیم که قبل از بوجود آمدن نسبیت ، تبدیلات گالیله به عنوان یک رابطه تبدیل خوب محسوب می‌گردید. و تنها در توجیه نتایج الکترومغناطیس با شکل مواجه شد. بنابراین با پیدایش ، ضرورت ایجاد یک تبدیل مناسب در فیزیک احساس می‌شد. بنابراین جهت برآوردن این نیاز ، تبدیلات لورنتس بوجود آمد. بنابراین می‌توان گفت که نظریه نسبیت ، نسبت به مکانیک کلاسیک که بر اساس قوانین نیوتن بنا نهاده شده بود، حالت کلی و جامع‌تر داشت.
  
  
• اصل توافق بیان می‌کند که یک نظریه عامتر باید در حالت جدی به نظریه قبلی تبدیل شود. و این اصل در مورد نظریه نسبیت برقرار است. یعنی اگر سرعت ذره در مقایسه با سرعت نور خیلی کوچک باشد، به راحتی و با خیال راحت می‌توانیم از قوانین نیوتن و مکانیک کلاسیک برای تشریح حرکت ذره استفاده کنیم.
  
  
• از طرف دیگر تبدیلات لورنتس نیز که نسبت به تبدیلات گالیله حالت عامتری دارد، بر اساس اصل فوق باید در حالت حدی به تبدیلات گالیله تحویل گردد. و اگر روابط مربوط به تبدیلات لورنتس را در نظر بگیریم ملاحظه می‌شود که در حالت حدی که سرعت ذره در مقایسه با سرعت نور خیلی کوچک باشد، تبدیلات لورنتس به تبدیلات گالیله تحویل می‌گردد. به عبارت دیگر می‌توان گفت که درست بعد از اینکه تبدیلات لورنتس برای توصیف صحیح انتشار نور از نظر ناظر در حال حرکت پذیرفته شد، دقت و تقریبی که به طور پنهان در قوانین مکانیک کلاسیک نیوتن وجود داشت، صرفا به عنوان نتیجه‌ای از کشف تبدیلات لورنتس به دست آمد.

شرط تعامد تبدیلات لورنتس

• تبدیلات لورنتس که رابطه بین مختصات مکانی و زمانی یک رویداد را در چارچوب مرجع لخت که نسبت به یکدیگر با سرعت ثابت حرکت می‌کند، بدست می‌دهد. اما این تبدیل متعامد نیست. تعامد را اینگونه می‌توان تشریح کرد که اگر مختصات مکانی و زمانی یک رویداد را در هر چارچوب مرجع با یک ماتریس ستونی نمایش دهیم، در اینصورت رابطه تبدیل به صورت یک ماتریس 4x4 خواهد بود که هرگاه ماتریس مختصات رویداد در یک چارچوب را در آن ضرب کنیم، مختصات همان رویداد در چارچوب دیگر که نسبت به چارچوب اول با سرعت یکنواخت حرکت می‌کند، حاصل می‌گردد. این ماتریس به عنوان ماتریس تبدیل معروف است.
  
  
• حال اگر مختصات مکانی و زمانی یک رویداد را بصورت (t, x, y, z ) در نظر بگیریم، تبدیلات لورنتس متعامد نخواهد بود. برای حل مشکل مینکوسکی (Minkowski) ترفند استفاده از مختصه زمان موهومی را پیشنهاد کرد. به عبارت دیگر مختصات مکانی زمانی یک رویداد باید به صورت (ict,x,y,z) فرض شود. بنابراین تبدیلات لورنتس از نوع مینکوسکی متعامد خواهد بود.
  
  
• لازم به ذکر است که نباید به کمیت‌های موهومی که در قالب مختصات مینکوسکی (یک دستگاه متعامد قراردادی چهار بعدی) ظاهر می‌شوند. اهمیت فیزیکی قائل شد. زیرا اینها صرفا نتیجه اعمال ترفند ریاضی در نوشتن مختصات یک رویداد است.

ناوردایی عنصر جهان – خط

از فیزیک نوین می‌دانیم که در سرعتهای نزدیک به سرعت نور ، کمیت‌های طول ، زمان ، جرم دیگر مفهوم کلاسیکی مطلق بودن خود را به طور کامل از دست داده و تابع سرعت می‌باشند. به گونه‌ای که انقباض طول ، اتساع زمان و افزایش جرم ملاحظه می‌گردد. اما در عوض کمیتی به نام عنصر جهان خط وجود دارد که مستقل از سرعت بوده و یک کمیت ناوردا می‌باشد. شرط ناوردایی این کمیت تحت تبدیلات لورنتس ایجاب می کند که اگر مختصات فضا زمان یک رویداد را بصورت (t, x, y, z ) نشان دهیم، این کمیت ناوردا بصورت زیر باشد.

کمیت فوق در چارچوبهای لخت ناوردا است. معلوم می‌شود که هرگاه کمیت فوق با نقاط واقع در مسیر باریکه نور در حال انتشار متناظر باشد، ناظرهای واقع در تمام چارچوبهای لخت مقدار ثابت مشابهی را برای آن ثبت می‌کنند.


همچنین ملاحظه کردیم که به منظور استفاده از مزایای دستگاه متعامد و خواص تبدیل آنها در مختصات چهار بعدی رویدادها در فضا - زمان مینکوسکی ترفند استفاده از مختصه زمانی موهومی را پیشنهاد کرد. به عبارت دیگر مختصات فضا - زمان یک رویداد را باید به صورت (ict,x,y,z) نمایش دهیم. 
 

 دیسک اسرار آمیز
وقتی که از چرخ و فلک پیاده می شوید، چه اتفاقی می افتد ؟

وسایل مورد نیاز

• مقوا
• چسب مایع یا نواری
• دیسک نمونه
• یک وسیله ی چرخنده ( گرامافون ، مته برقی با سرعتهای مختلف ، مته دستی و یا غیره )

شرح آزمایش

از تصویر دیسک اسرار آمیز یک کپی تهیه کرده و با استفاده از چسب نواری یا چسب مایع روی مقوای دایره شکلی بچسبانید و سپس مقوای دایره شکل را به مرکز وسیلهُ چرخانتان وصل کنید . دستگاه گرامافون با دوره چرخش 45 یا 78 دوردر دقیقه برای این کار بسیار مناسب است . بعد از اینکه وسیله ی چرخنده را به گردش درآوردید ، به مدت 15 ثانیه به مرکز دیسک نگاه کنید .
سپس نگاه خود را از دیسک برداشته و به دیواریا شخص نزدیکی بنگرید . توجه کنید که شخص یا دیوار به نظر منقبض و یا منبسط می شوند ، به نظر می رسد که شخص مورد نظر به سمت شما هجوم می آورد یا از شما دور می شود.
اگر می توانید تلاش کنید تا دستگاه چرخنده خود را در جهت مخالف به چرخش درآورید. حالا وقتی نگاه خود را از دیسک برمی دارید چه اتفاقی می افتد ؟

چه اتفاقی در حال وقوع است؟

سیستم دیداری شما به حرکاتی که به سمت درون یا بیرون باشد حساس است . وقتی به اجسامی که به مرکز میدان دیدتان نزدیک یا دور می شوند می نگرید ، سلولهای عصبی ای که در قشای دیداری شما قرار دارند، بیشتر تحت تاُ ثیر قرار می گیرند . با نگاه کردن به یک جسم ساکن ، سیگنال هایی با یک قدرت به مغز شما می رسد و وقتی شما به جسم در حال حرکتی خیره می شوید ، قسمتی از این سلولها خسته می شوند و وقتی به دیوار خیره شوید قسمت دیگری از سلولها که کار نکرده اند ، سیگنالهای قوی تری نسبت به قسمت خسته، به مغز ارسال می کنند .
بطور مثال اگر وسیله ی گرداننده در جهت دور شدن از شما ، می چرخد ، وقتی نگاهتان را از آن بر می دارید و به دیوار نگاه می کنید ، بنظر می رسد که دیوار به شما نزدیک می شود . وقتی دستگاه گردانتان را در خلاف جهت بگردانید ، آنگاه بنظر می رسد که جسم به شما نزدیک، و دیوار از شما دور می شود .

ضمیمه

کنار آبشاری بایستید و به نقطه ای درون آبشار بمدت یک دقیقه بنگرید . سپس به صخره ای کنار آبشار نگاه کنید . چه چیزی می بینید؟
خواهید دید که صخره به سمت بالا می رود . این حرکت ظاهری مربوط به خستگی بخشی از سیستم دیداری شما می شود که حرکت بالا رونده و پایین رونده را آشکار می کند.

نگاه اجمالی

دریای شیطان کجاست؟

وجه اشتراک مثلث برمودا و دریای شیطان

سخن اخر

• آیا ارتباطی بین مثلث برمودا و دریای شیطان وجود دارد؟
  
  
• آیا می‌توان مفقود شدنهای کشتیها و هواپیماها در این مناطق را به حوادث طبیعی نسبت داد؟
  
  
• یعنی امکان دارد آتشفشانهای زیر دریا ، امواج جزر و مدی یا زمین لرزه‌های زیر آب باعث ناپدید شدن کشتیها از روی دریا و حتی هواپیماها گردند؟ در این صورت با وجود ابزارهای پیشرفته و جتسجوهای فروان حداقل باید اثری از مفقودین یا گزارشی از حوادث مزبور وجود می‌داشت. پس معمای دریای شیطان را هم باید به گنجینه اسرار حل نشدنی جهان هستی اضافه کنیم، مگر اینکه پاسخی قانع کننده ، برای آن بیابیم.

در این مبحث هواپیماها و کشتیهای مهمی که تا سال 1974 در مثلث برمودا ناپدید شده‌اند، را لیست کرده‌ایم.

هواپیماهای مهم مفقود شده

1. 5 دسامبر 1945 : 5 هواپیمای جنگنده TBM متعلق به نیروی دریایی که در یک پرواز آموزشی از پایگاه دریایی هوایی فورت لادردیل در فلوریدا به هوا برخاستند و همگی ناپدید شدند. مجموع خلبان و سرنشینان آن 14 نفر بودند.
   
   
2. 5 دسامبر 1945 : هواپیمای بمب افکنهای PBM مارتین مارینر با 13 خدمه که جهت نجات هواپیماهای TBM اعزام شده بود، چند دقیقه بعد از پرواز ارتباط رادیویی‌اش قطع شده و ناپدید گشت.
   
   
3. 1947 : هواپیمای سوپر فورت C-54 متعلق به ارتش آمریکا در 100 مایلی برمودا ناپدید شد.
   
   
4. 29 ژانویه 1948 : هواپیمای چهار موتوره استارتایگر از نوع تئودور 4 در حالیکه ارتباط رادیویی‌اش با مرکز قطع گردیده بود، در 380 مایلی شمال شرقی برمودا با 13 سرنشین و خدمه گم شد.
   
   
5. 28 دسامبر 1948 : هواپیمای Dc-3 در مسیر سن خوان به میامی با 32 سرنشین به اضافه خدمه ناپدید شد.
   
   
6. 17 ژانویه 1949 : استارآریل همتای هواپیمای استارتایگر ، در مسیر لندن به سانیتاگوی شیلی از طریق برمودا و جامائیکا ، در 380 مایلی جنوب و جنوب غربی برمودا سمت کینگستون پس از قطع ارتباط رادیویی‌اش ، ناپدید شد.
   
   
7. مارس 1950 : هواپیمای آمریکای گلوب ماستر در شمالی‌ترین قسمت مثلث در حالیکه رهسپار ایرلند بود، گم شد.
   
   
8. 2 فوریه 1952 : هواپیمای باربری انگلیسی یورک در شمال مثلث که رهسپار جامائیکا بود، با 33 سرنشین ، ناپدید شد.
   
   
9. 30 اکتبر 1954 : هواپیمای نیروی دریایی سوپر کانستلیشن با 40 سرنشین در شمال مثلث ناپدید گشت.
   
   
10. 9 نوامبر 1956 : هواپیمای گشتی P5M متعلق به نیروی دریایی با 10 خدمه نزدیک برمودا ناپدید شد.
    
    
11. 8 ژانویه 1962 : هواپیمای نیروی هوایی در مسیر لنگلی فیلد ، در ویرجینیا به آزورز ، گم شد.
    
    
12. 28 آگوست 1963 : دو هواپیمای جدید متعلق به نیروی هوایی ، چهار موتوره از نوع KC- 135 استراتوتانکرز از پایگاه هوایی همستید ، در فلوریدا به قصد پیوستن به گروه اختصاص یافته جهت سوخت گیری ، در 300 مایلی جنوب غربی برمودا ناپدید شد.
    
    
13. 5 ژوئن 1965 : هواپیمای C- 119 باکسکار با 10 خدمه در جنوب شرقی باهاما ناپدید گردید.
    
    
14. 11 ژانویه 1967 : هواپیمای YC- 122 شکاری که به هواپیمای باری تبدیل شده بود، با 4 سرنشین در ناحیه گلف استریم بین پالم‌بیج و گراند باهاما گم شد.
    
    
15. 22 سپتامبر 1963 : هواپیمای بازی C-132 که رهسپار آزوزر بود، ناپدید گشت.

کشتیهای مهم مفقود شده

لیست زیر کشتیهای مهمی که در مثلث برمودا ناپدید شده‌اند یا بدون هیچ سرنشینی به حالت غرق شده در آبها پیدا شده‌اند، را نشان می‌دهد.

1. 1840 : کشتی بزرگ فرانسوی رزالی که از اروپا عازم هاوانا بود، در مثلث برمودا با تمام وسایل دریانوردی و مجموعه‌های دست نخورده پیدا شد، در حالی که تمام سرنشینان آن ناپدید شده بودند.
   
   
2. ژانویه 1880 : کشتی جنگی بادبان‌دار انگلیسی آتلانتا ، برمودا را به مقصد انگلستان با 290 سرنشین ترک کرد که احتمالا در محلی نه چندان دور از برمودا باید ناپدید شده باشد.
   
   
3. اکتبر 1902 : کشتی آلمانی سه دکله فریا ، مدت زمانی کوتاه بعد از ترک مانزانیوی کوبا در حالیکه خیلی ناجور کج شده و قسمتی از دکل آن از بین رفته و لنگر آن آویزان بود، پیدا شد. تقویم اتاق کاپیتان 14 اکتبر یعنی روز بعد از حرکت را نشان می‌داد.
   
   
4. مارس 1918 : کشتی نیروی دریایی آمریکا به نام یواس. اس سیکلوپز ، 19000 تنی با طول 500 پا در چهارم مارس از باربادوس با 309 سرنشین و خدمه به طرف نورفولک حرکت کرد. نه هوا بد بود، نه پیامی رادیویی دریافت شد و نه قطعه شکسته‌ای هرگز از آن بدست آمد.
   
   
5. 1925 : اس. اس. کاتوپاکسی که از چارلستون عازم هاوانا بود، ناپدید گردید.
   
   
6. آوریل 1932 : دو کشتی دکل‌دار جان و مری ، ثبت شده در نیویورک ، شناور اما خالی از سرنشین در 50 مایلی جنوب برمودا در حالیکه بادبانهایشان جمع شده بود و بدنه آنها به تازگی نقاشی گردیده بود، پیدا شدند.
   
   
7. فوریه 1940 : کشتی گلوریا کلیت از سینت وینسنت ، متعلق به کمپانی هند غربی ، بدون سرنشین از 200 مایلی جنوب موبایل در آلاباما پیدا شد، در حالیکه همه وسایل آن دست نخورده و منظم بود.
   
   
8. 22 اکتبر 1944 : کشتی باری کوبایی به نام رابیکن در حالی که همه سرنشینان آن به به جز یک سگ ، به نظر می رسید که کشتی را ترک کرده‌اند، بوسیله گارد ساحلی در گلف استریم از سواحل فلوریدا پیدا شد.
   
   
9. ژوئن 1950 : کشتی باری اس. اس. سندرا به طول 350 پا از ساوانای جورجیا به مقصد پورتو کابلو ، در ونزوئلا با 300 تن محموله حشره‌کش از سینت آگوستین در فلوریدا ، عبور کرد و سپس بدون باقی گذاشتن هیچ اثری از خود ناپدید گردید.
   
   
10. سپتامبر 1955 : کشتی کانمارا 4 به طرزی مرموز در 400 مایلی جنوب غربی برمودا غرق شده بود.
    
    
11. 2 فوریه 1963 : کشتی باری مارین سولفور کوئین به طول 425 پا که از بیومونت در تگزاس رهسپار نورفولک در ویرجنیا بود، بدون ارسال هیچ پیامی اثری یا باقی گذاشتن شکسته پاره‌ای از خود با تمام خدمه و سرنشینان ناپدید شد.
    
    
12. اژوئیه 1963 : کشتی کوچک ماهیگیری اسنو بوی با 63 پا طول و 40 سرنشین ، در جامائیکا به مقصد شمال شرقی کی ، در 80 مایلی جنوب برمودا ناپدید گشت.
    
    
13. 1924 : کشتی باری ژاپنی ری فوکو مارو در فاصله‌ای بین باهاما و کوبا تقاضای کمک کرد و سپس ناپدید شد.
    
    
14. 1931 : کشتی باری استیونجر با 43 خدمه ناپدید گردید.
    
    
15. مارس 1938 : کشتی باری استرالیایی آنجلو استرالین با 39 خدمه ، خبری را بدین مضمون "همه چیز خوب است" برای آخرین بار از آزورز مخابره کرد.
16. دسامبر 1967 : قایق مسابقه‌ای رواناک با 46 پا طول در حالیکه از خشکی اطراف قابل روئیت بود، ناپدید گردید.
    
    
17. 24 دسامبر 1967 : کشتی ویچ کرافت به حالت شناور در بندری در یک مایلی میامی پیداش شد، در حالیکه کابین هدایت کشتی سرنشینان و مالک آن همگی ناپدید شده بودند.
    
    
18. آوریل 1970 : کشتی باری میلتون یاتریدز که از نیو اورلئان عازم کیپ تاون بود، ناپدید شد.
    
    
19. مارس 1973 : کشتی باری هزار تنی آنتیا که با 32 خدمه در مسیر نیوپورت نیوز به آلمان در حال دریانوردی بود، ناپدید گردید.

مثلث برمودا

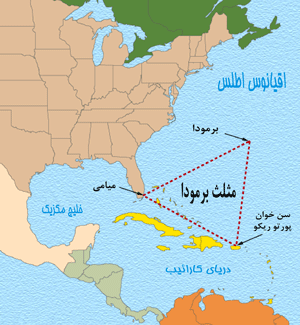موقعیت مثلث برمودا

مثلث برمودا واقعا یک مثلث نیست، بلکه شباهت بیشتری به یک بیضی (و شاید هم دایره‌ای بزرگ) دارد که در روی بخشی از اقیانوس اطلس در سواحل جنوب شرقی آمریکا واقع است. راس آن نزدیک برمودا و قسمت انحنای آن از سمت پایین فلوریدا گسترش یافته و از پورتوریکو گذشته ، به طرف جنوب و شرق منحرف شده و از میان دریای سارگاسو عبور کرده و دوباره به طرف برمودا برگشته است. طول جغرافیایی در قسمت غرب مثلث برمودا 80 درجه است، بر روی خطی که شمال حقیقی و شمال مغناطیسی بر یکدیگر منطبق می‌گردند. در این نقطه هیچ انحرافی در قطب نما محاسبه نمی‌شود.

وینسنت گادیس که مثلث برمودا را نامگذاری کرده، آن را به صورت زیر توصیف می‌کند: « یک خط از فلوریدا تا برمودا ، دیگری از برمودا تا پورتویکو می‌گذرد و سومین خط از میان باهاما به فلوریدا بر می‌گردد. »

این محل فتنه‌انگیز و تقریبا باور نکردنی اسرار غیر قابل توصیف جهان را به خود اختصاص داده است. مثلث برمودا نامش را در نتیجه ناپدید شدن 6 هواپیمای نیروی دریایی همراه با تمام سرنشینان آنها در پنجم دسامبر 1945 کسب کرد. 5 فروند از این هواپیماها به دنبال اجرای ماموریتی عادی و آموزشی ، در منطقه مثلث ، پرواز می‌کردند که با ارسال پیامهایی عجیبی درخواست کمک کردند. هواپیمای ششم برای انجام عملیات نجات ، به هوا برخاست که هر شش هواپیما به طرز فوق‌العاده مشکوکی مفقود شدند.

آخرین پیامهای مخابره شده آنها با برج مراقبت حاکی از وضعیت غیر عادی ، عدم روئیت خشکی ، از کار افتادن قطب نماها یا چرخش سریع عقربه آنها و اطمینان نداشتن از موقعیتشان بود. این در حالی بود که شرایط جوی برای پرواز مساعد بود و خلبانان و دیگر سرنشینان افرادی با تجربه و ورزیده بودند. با وجود مدتها جستجو هیچ اثری از قطعه شکسته ، لکه روغن ، آثاری از اجسام شناور ، خدمه یا تجمع مشکوکی از کوسه‌ها دیده نشد. هیچ حادثه‌ای چه قبل و چه بعد از آن ، تا این حد حیرت‌آورتر از ناپدید شدن دسته جمعی هواپیماهای مذکور نبوده است. در حوادثی مشابه در این منطقه ‌قایقها و کشتیهایی مفقود شده‌اند (قربانیان مثلث برمودا)، در برخی موارد هم فقط خدمه و سرنشینان ناپدید گشته‌اند.

منطقه وحشت

همه روزه هواپیماهای متعددی بر فراز مثلث برمودا پرواز می‌کنند. کشتیهای بزرگ و کوچک در آبهای آن در حال تردند و افراد زیادی برای بازدید ، به این منطقه مسافرت می‌کنند، بدون آنکه اتفاقی بیفتد. از طرف دیگر ، در دریاها و اقیانوسها در سراسر دنیا ، کشتیها و هواپیماهای زیادی مفقود شده و می‌شوند. پس چرا فقط مثلث برمودا از بقیه مناطق تفکیک شده است. علت این است که اولا هیچ امیدی برای یافتن حتی اثر و نشانه‌ای وجود ندارد. ثانیا در هیچ منطقه دیگر چنین ناپدید شدنهای بی دلیل ، بیشمار و نامعلوم روی نداده و به این خوبی ثبت نشده است.

مشاهدات و گزارشات

در بیشتر اتفاقات مثلث برمودا ، اکثر هواپیماها در حالی ناپدید شده‌اند که تماس رادیویی خود را با ایستگاههای مبدا و مقصدشان تا آخرین لحظه حفظ کرده‌اند و یا برخی دیگر در لحظات آخر پیامهای غیر عادی مخابره کرده‌اند که حاکی از عدم کنترل آنان بر روی دستگاه و ابزارها بوده است و یا چرخش عقربه‌های قطب نما به دور خود و تغییر رنگ آسمان اطراف به زردی و مه آلودی ، آن هم در روز صاف و آفتابی و یا تغییراتی غیر عادی در آبها که تا لحظاتی قبل آرام بوده‌اند، بدون بیان هیچ دلیل روشنی از چگونگی این وقایع.

این پیامها رفته رفته ضعیف‌تر و غیرقابل تشخیص‌تر شده و یا سریعا قطع شده‌اند. دقیقا مثل اینکه چیزی ارتباط رادیویی را قطع کرده باشد و یا چنانچه اظهار عقیده شده، در حال دور شدن و عقب رفتن از فضا و زمان بوده و دورتر و دورتر شده‌اند. در برخی موارد گزارشها حاکی از آن بود که نوری ناشناخته و غیر قابل تشریح روئیت شده است. همچنین توده سیاه و تاریکی در سطح دریا که پس از مدتی ناپدید شده ، در جریان اتفاقات مزبور گزارش شده است.

در مواردی هم گزارش شده که نقطه تاریک بزرگی در میان ستارگان در آسمان دیده شده که نوری متحرک از طرف زمین به آن قسمت وارد شده و سپس هر دو ناپدید شده‌اند. در تمام مدت دیده شدن تاریکی ، دستگاهها و سایر ابزارهای قایق‌های ناظر از کار افتاده بودند که پس از رفع تاریکی آسمان ، دوباره شروع بکار کرده‌اند.

در یک مورد هم پیامی عجیب از یک کشتی باری ژاپنی بدین مضمون دریافت گردید. "خطری همانند یک خنجر هم اکنون ... به سرعت می‌آید ... ما نمی‌توانیم فرار کنیم ..." در هر حال بدون اینکه مشخص شود خنجر چه بود، کشتی ناپدید شد.

علل واقعه

علل فرضی طبیعی

توضیحات و علل فرضی مختلفی درباره حوادث مثلث برمودا ارائه شده است که معمول‌ترین فرضیات بر اساس مرگ غیر طبیعی (زیرا هیچ جسدی تا کنون بدست نیامده است.) بنا شده است. این توضیحات عبارتند از:

جزر و مد ناگهانی دریا در نتیجه زلزله در اعماق دریا ، وزش بادهای مخرب و اختلالات جوی ، گویهای آتشفشان که موجب انفجار هواپیماها می‌شود، گرفتار آمدن در جاذبه یک گرداب یا گردباد که باعث سقوط و انهدام هواپیماها یا انحراف مسیر کشتیها و مفقود شدن آنها در آب می‌شود، تحت تاثیر نیرویی مغناطیسی قرار گرفتن و اختلالات امواج الکترومغناطیسی، ولی این دلایل توجیه قابل قبولی برای ناپدید شدن هواپیماها و کشتیهای متعدد در یک منطقه نیست.

علل فرضی غیر طبیعی

دستگیری و ربوده شدن به وسیله زیردریایی یا بشقاب پرنده‌هایی متعلق به کراتی دیگر که برای تحقیق درباره حیات و زندگی باستان و حال ما انسانها به کره زمین آمده‌اند، می‌تواند علتی غیر طبیعی برای توجیه وقایع باشد.

یکی از عجیب‌ترین پیشنهادات در این مورد بوسیله ادگار کایس ، پیشگو و روانکاو و حکیم در دهه پنجم قرن بیست ، ارائه شده است. به عقیده وی قرنها قبل از کشف اشعه لیزر ، بومیان سواحل اقیانوس اطلس از کریستال به عنوان یک منبع انرژی و قدرت استفاده می‌کردند. به نظر کاین نوعی نیروی شیطانی القا شده از سوی آنها ، در عمق یک مایلی در قسمت غرب اندروس غرق شده که هنوز در برخی مواقع باعث از کار انداختن ابزار و وسایل الکتریکی کشتیها ، هواپیماها و در نهایت نابودی آنها می‌گردد.

ام. ک. جساپ که یک فضانورد ، منجم و متخصص کره ماه است، در کتابش به نام « در مورد بشقاب پرنده‌ها » ابزار می‌دارد که ناپدید شدن کشتیهای مشهور در مثلث برمودا ، به وسیله اجسام پرنده صورت گرفته است. وی مفقود شدن خدمه آنها را نیز به اجسام مزبور ربط می‌دهد. به عقیده جساپ یوفوها هر چه هستند، حوزه مغناطیسی موقتی ایجاد می‌کنند که دارای طرحی یونیزه شده است و می‌تواند باعث متلاشی شدن یا ناپدید شدن هواپیماها و کشتیها گردد. او روی این سوال کار می‌کرد که چگونه نیروی مغناطیسی کنترل شده و می‌تواند باعث نامرئی شدن گردد. نظریه میدان واحد انیشتین او را مجذوب کرده بود. جساپ هر دو اینها را کلیدی می‌دانست برای ظهور و محو شدن ناگهانی بشقاب پرنده‌ها و ناپدید شدن کشتیها و هواپیماها. ولی مرگ امکان ادامه فعالیت و نتیجه گیری را از جساپ گرفت و تحقیقاتش نیمه تمام ماند.

داستانی عجیب

حادثه‌ای در اثر اختلال زمانی در فرودگاه میامی رخ داد که هرگز توضیحی قابل قبول برای آن وجود نداشته است. این واقعه مربوط به یک هواپیمای مسافربری بود که برای فرود در باند آماده بود و با رادار مرکز کنترل هوایی ردیابی می‌گردید که ناگهان ده دقیقه از صفحه رادار ناپدید شد و سپس دوباره ظاهر گشت. هواپیما بدون هیچ واقعه‌ای فرود آمد و خلبان و خدمه از آنچه افراد پایگاه می‌گفتند ابراز تعجب کردند، زیرا تا آنجا که به خدمه مربوط می‌شد، هیچ اتفاق غیر عادی نیفتاده بود. جالب این که ساعتهای همه آنها حدود ده دقیقه از زمان واقعی عقب‌تر بود. در حالی که هواپیما درست 20 دقیقه قبل از این واقعه وقت اصلی را کنترل کرده بود و در آن هنگام هیچ اختلاف زمانی وجود داشت.

• آیا مثلث برمودا و نقاط مشخص دیگر به صورت ماشینی عظیم عمل می‌کنند تا اختلالاتی بوجود آورند؟
  
  
• آیا آنها می‌توانند گردابهایی را چه در داخل و چه در خارج از جو بوجود آورند که اجسام و اشیا به داخل آنها بیفتد و به بعد زمان و مکانی دیگر منتقل شوند؟

گذشته و آینده برمودا

به نظر می‌رسد که این منطقه طی زمانهای متمادی گذشته نیز در افسانه‌ها به منزله مکانی ترسناک وجود داشته و حتی خیلی قبل از تاریخ کشف آن و بعد از آن تاریخ تا صدها سال با عناوین «دریایی از مقبره‌ها» ، «مثلث شیطان» ، «مثلث مرگ» ، «دریای بدبختی» ، «گورستان آتلانتیک» نامیده می‌شده است.
شومی و بدشگونی مثلث برمودا حتی در عصر فضا نیز باعث تعجب انسانهایی چون کریستف کلمب و فضانوردان آپولو 13 که یکی کاشف در زمین و دیگری در فضاست، شده است.

اینکه چرا وقایع عجیب این منطقه گزارش نمی‌شود، شاید به دلیل ایجاد رعب و وحشت عمومی باشد، شاید هم چون دلیل اصلی وقایع معلوم نیست، اتفاقات مربوطه بازتاب نمی‌یابد. البته در اغلب گزارشات ارائه شده هم سانسورهایی وجود دارد که اصل وقایع را سرپوشیده نگه می‌دارد.

• آیا این مثلث دوباره قربانیان دیگری می‌گیرد؟
  
  
• آیا بشر موفق به کشف راز آن خواهد شد؟

و بسیاری آیاها و پرسشهای بی جواب دیگر که مسلما در ذهن شما هم وجود دارد

آیا تاکنون فکرکرده اید که چرا برخی چیزها درون آب شناور هستند امابرخی دیگر ته آب میافتند؟

یا چرا چوب روی آب شناور ولی یک میخ آهنی ته ظرف آب می افتد و یااینکه آیا امکان دارد یک قطعه آهن شناوربماند تمامی این موضوعات به نیرویی مربوط می شود که ارشمیدس دانشمند یونان باستان کشف کرده است.

نیروی ارشمیدس چیست ؟
وقتی جسمی را درون یک شاره مثلا یک لیوان آب می اندازیم اگر جسم تماما درون آب فرو رود به مقدار حجم خود آب را جابجا می کند به نیروی وزن این مقدار آب جابجا شده نیروی ارشمیدس گویند که همیشه رو به بالاست و از رابطه ی زیر بدست می آید:

 

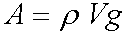
دقت کنید که در این رابطه چگالی شاره و vحجم شاره جابجا شده است که مساوی است باحجم قسمتی از جسم که داخل شاره است و gشتاب گرانشی است حال سوالی مطرح می شود و آن اینکه چه شرایطی لازم است تا یک جسم در یک شاره شناور شود ؟ می دانیم در به هر جسمی در یک میدان گرانشی نیروی وزن وارد می شود و به جسم درون شاره حداقل دو نیروی ارشمیدس و نیروی گرانش وارد می شود می دانیم که نیروی گرانش همیشه روبه پایین و نیروی ارشمیدس (نیروی شناوری) همیشه روبه بالا هرگاه این دو نیرو برابر باشند جسم درون آب غوطه ور می شود ولی فرق شناوری و غوطه وری چیست ؟ وقتی می گوییم جسمی شناور است که در سطح آب باشد اما جسم غوطه ور میتواند در هر جای شاره باشدبه طور مثال خود آب درون خود شناور است.

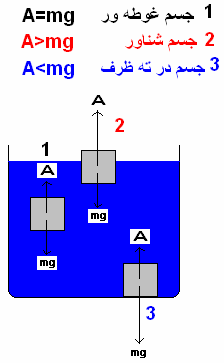
وقتی نیروی ارشمیدس از نیروی وزن بیشتر باشد جسم روی سطح آزاد شاره شناور می شود و وقتی نیروی وزن جسم از نیروی ارشمیدس بیشتر باشد جسم درون شاره غرق می شود.

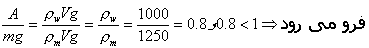
مثال:آیاجسمی به چگالی 1250 kg/m³ روی آب شناور می ماند؟ و مقدار نیروی ارشمیدس این ماده را برای³ 1m از این ماده به دست آورید.
(ب)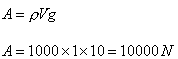
 

مثال (2) نیروی شناوری را برای آهن mکه در جیوه شناور است بدست آورید .

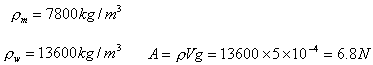
با توجه به اینکه نیروی وزن این قطعه آهن 3.9 اسحاق نیوتن است پس حتی آهن نیز روی جیوه شناور می ماند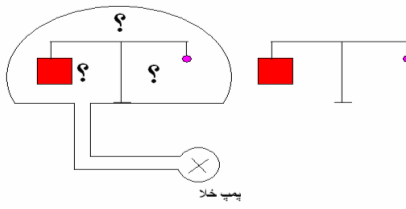

مسئله : این دو جسم در هوا روی یک ترازوی این چنین به تعادل می رسند اگر آنها را در یک محفظه خلا بگذاریم موقعیت آنان چگونه است ؟(راهنمایی:هوا نیز یک شاره است)

موضوع چیست؟

همه ما تا کنون به نحوی قانون ارشمیدس را تجربه کرده‌ایم. قانون ارشمیدس می‌گوید: وقتی جسمی درون سیالی (مایع یا گاز) قرار می‌گیرد. نیرویی برابر وزن سیال جابجا شده ، از طرف سیال ، بر جسم وارد می‌شود. هر گاه جسمی درون آب قرار می‌گیرد، وزن آن کمتر از موقعی است که در هوا باشد، به همین جهت است که وقتی در استخر شنا می‌کنید احساس می‌کنید که وزنتان کاهش یافته است.

این یک شوخی نیست!

همه این سوال را شوخی آمیز می‌دانند! یک تن چوب سنگین‌تر است یا یک تن آهن و معمولا بدون اینکه فکر کنند می‌گویند: البته یک تن آهن و موجب خنده دسته جمعی اطرافیان می‌شوند. اگر به آدمهای شوخ جواب دهند که یک تن چوب از یک تن چوب آهن سنگین‌تر است، لابد آنها بلندتر خواهند خندید چون ظاهر این جواب با هیچ منطقی جور در نمی‌آید، اما این حرف درست است.

حقیقت چیست؟

حقیقت مطلب در آن است که قانون ارشمیدس نه فقط در مورد مایعات ، بلکه در مورد گازها نیز صدق می‌کند. وزن هر جسمی در هوا به اندازه وزن هوای هم حجم آن کم می‌شود. از وزن چوب و آهن نیز در هوا قدری کاسته می‌شود. برای آنکه وزن حقیقی چوب و آهن را بدانیم باید آنچه را که از وزن هر یک کاسته شده است، به آن اضافه کنیم.

بنابراین در مثال ما ، وزن حقیقی چوب مساوی است با یک تن + وزن هوای هم حجم چوب. و وزن حقیقی آهن مساوی است با یک تن + وزن هوای هم حجم آهن. اما حجم یک تن چوب به مراتب (تقریبا 15 بار) بیشتر از یک تن آهن است. به همین جهت ، وزن حقیقی یک تن چوب بیشتر از وزن حقیقی یک تن آهن است! برای آنکه جواب دقیق‌تری داده باشیم. باید بگوییم: وزن حقیقی چوبی که در هوا یک تن وزن دارد از وزن حقیقی آهن که در هوا یک تن وزن دارد، بیشتر است.
چون حجم یک تن آهن 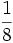متر مکعب و حجم یک تن چوب در حدود 2 متر مکعب است، پس تفاوت وزن هوای هم حجم آنها باید در حدود 2.5 کیلوگرم باشد. به این ترتیب ، یک تن چوب ، در واقع به همین اندازه از یک تن آهن سنگین‌تر است!

• سوخت های فسیلی
• انواع دیگر انرژی
• انواع شتاب دهنده
• در حوزه ذرات
  
  
  
  
  امروز سوخت و انرژی در دنیا به چند دسته کلی تقسیم می شوند. سوخت های فسیلی و سوخت های غیرفسیلی و انرژی های تجدید پذیر و غیرقابل تجدید.

سوخت های فسیلی

سوخت های فسیلی عبارتند از: نفت، گاز و زغال سنگ که با اکسیژن هوا ترکیب می شوند و ایجاد انرژی به شکل حرارت می کنند. این سوخت ها در مقایسه با سوخت های دیگر انرژی کمتر تولید می کنند. مثلاً یک کیلوگرم زغال سنگ حدود ۸ کیلووات ساعت انرژی تولید می کند و یک کیلوگرم نفت حدود ۱۲ کیلووات ساعت انرژی تولید می کنند. این سوخت ها آلوده کننده محیط زیست نیز هستند.

به علاوه جزء ذخایر غیرقابل تجدید بوده و دارای مشکلات زیادی در حمل و نقل ایمنی نیز هستند. مانند گازگرفتگی (خفگی) یا تولید گاز سمی منوکسید کربن. دسته دیگر از سوخت ها شامل سوخت های هسته ای هستند مانند اورانیوم یا پلوتونیوم یا ایزوتوپ های هیدروژن مانند دوتریوم یا تریتیوم یا فلز سبک لیتیوم. این سوخت ها در مقایسه با سوخت های دسته اول دارای امتیازات مثبت و منفی هستند. اول اینکه در این سوخت ها بعضی ایزوتوپ ها توانایی تولید انرژی به وسیله تکنولوژی فعلی بشر را دارد مانند ایزوتوپ های کمیاب اورانیوم ۲۳۵ یا پلوتونیوم ۲۳۹ یا اورانیوم ۲۳۳ که به این ایزوتوپ ها شکاف پذیر می گویند. امتیازات اینها عبارتند از تولید مقادیر زیاد انرژی به وسیله حجم کم ماده سوختنی. مثلاً از یک کیلوگرم اورانیوم ۲۳۵ یا پلوتونیوم ۲۳۹ می توان مقدار ۲۳میلیون کیلووات ساعت گرما ایجاد کرد، اما مشکلاتی نیز دارند از آن جمله این که: غنی سازی و تولید این ایزوتوپ ها مشکلات و هزینه زیادی دارند. دوم اینکه، این سوخت های هسته ای سنگین پس از تولید انرژی مقادیر زیادی ایزوتوپ های پرتوزا از خود به جای می گذارند که به زباله های هسته ای موسوم است.

این زباله ها برای محیط زیست و سلامت افراد خطرناک هستند و باید برای صدها سال در انبار های محکم نگهداری شوند تا رادیواکتیو آن از بین برود. دسته دیگر از سوخت های هسته ای شامل عناصر سبک مانند دوتریوم یا تریتیوم یا لیتیوم هستند که قرار است در راکتور های گداخت یا همجوش هسته ای تولید انرژی کنند. البته تاکنون از اینها در بمب های هیدروژنی بهره برداری نظامی و تسلیحاتی می شد، اما برای تولید انرژی برای مصارف صلح آمیز تکنولوژی راکتور های گداخت باید تکمیل شود، این سوخت ها معایب و مزایای فراوانی دارند. اول تولید نوترون و تشعشعات نوترونی می کنند که باید در راکتور های همجوشی هسته ای به نحوی جذب و کنترل شوند دوم اینکه تریتیوم نباید از راکتور نشت کند زیرا یک ایزوتوپ رادیواکتیو است.مزایای این سوخت ها عبارت از این که فراوان در دسترس هستند و دوم اینکه تولید انرژی زیادتری نسبت به اورانیوم یا پلوتونیوم می کنند. مثلاً انرژی حاصل از گداخت هیدروژن به هلیوم مساوی است با ۱۷۷میلیون کیلووات ساعت در صورتی که انرژی حاصل از اورانیوم برابر است با ۰۰۰/۰۰۰/۲۳ کیلووات ساعت. بنابراین یک کیلوگرم هیدروژن حدود ۸ برابر یک کیلوگرم اورانیوم تولید انرژی می کند.

انواع دیگر انرژی

انواع دیگر انرژی عبارتند از: انرژی خورشیدی، انرژی باد، انرژی زمین گرمایی و انرژی بیوگاز که مشکل بزرگ این انرژی تجدیدپذیر اینکه بازده انرژی اینها پایین است و دوم اینکه دائمی نیستند و سوم اینکه تکنولوژی بشر برای استفاده مقیاس زیاد از اینها تکمیل نیافته است. ما در این مقاله سعی می کنیم جدیدترین طرح تولید انرژی که شاید یکی از منابع انرژی قرن ۲۱ باشد را معرفی کنیم. این طرح تولید انرژی عبارت از شتاب دهنده ذرات اتمی برای تولید انرژی زیاد، عملکرد این سیستم و دستگاه براساس استفاده از میدان های الکتریکی و مغناطیسی برای شتاب دادن و کنترل ذرات باردار الکتریکی تا مرز سرعت نور است. این سیستم ها قادر هستند سرعت الکترون ها و پروتون ها را تا مرز سرعت نور شتاب دهند. وقتی ذرات تا این حد شتاب یافتند سطح انرژی آنها چند میلیون برابر می شود و دارای انرژی عظیم و فراوانی می شود. یک مثال نشان دهنده این مطلب است، به عنوان مثال شتاب دهنده پروتون در آزمایشگاه فرمی آمریکا قادر است ذرات پروتون را تا یک تریلیون الکترون ولت (Tev) شتاب دهد.

اگر ما به وسیله این شتاب دهنده پروتون های یک گرم هیدورژن معمولی که در آب زیاد است را تزریق کنیم و شتاب دهیم انرژی پروتون ها برابر خواهد بود با انرژی ۲۶ میلیارد کیلووات ساعت انرژی، که مساوی است با انرژی تولید شده به وسیله شکافت حدود ۱۲۰۰ کیلوگرم اورانیوم یا ۱۵ میلیون بشکه نفت. همه این انرژی عظیم و غیرقابل باور فقط به وسیله شتاب دادن پروتون های یک گرم هیدروژن تا سطح انرژی یک تریلیون الکترون ولت است. پس با این محاسبات دانستیم که شتاب دهنده ها دارای چه قدرت عظیمی هستند.

انواع شتاب دهنده

شتاب دهنده ها به چند دسته کلی تقسیم بندی می شوند:

1. شتاب دهنده های خطی
2. شتاب دهنده های مداری
3. شتاب دهنده سیلکووترون

علاوه بر آن ساخت و نگهداری شتاب دهنده آسان و کم هزینه است. در ضمن می توان این سیستم های مولد را در ابعاد و مقیاس های مختلف ساخت به عنوان مثال یک شتاب دهنده خطی که طول آن ۱۰۰ متر و ولتاژ آن ۱۰ میلیون ولت است که قادر است انرژی معادل یک گیگا (Gev) الکترون ولت تولید کند. این انرژی معادل است با انرژی ۲۶ میلیون کیلووات ساعت در هر ثانیه. اگر تنها موفق شویم ۵۰ درصد انرژی این شتاب دهنده را استفاده کنیم این شتاب دهنده قادر است معادل ۲۰ هزار نیروگاه اتمی در مقیاس نیروگاه اتمی هزار مگاواتی نیروگاه بوشهر تولید انرژی کند. یعنی قادر خواهد بود ۲۰ میلیون مگاوات انرژی الکتریکی تولید کند.

علاوه بر آن از حرارت و گرمای تولیدی این دستگاه می توان برای بخار کردن آب دریا و تولید آب شیرین استفاده کرد. محاسبات نشان می دهد که این سیستم قادر خواهد بود در سال معادل بارندگی سالیانه کشور آب شیرین تولید کند، بدون اینکه هوا را آلوده کند یا مشکلاتی از قبیل زباله های هسته ای یا پس مانده و آلودگی ایجاد کند، در واقع یکی از بهترین منابع انرژی خواهد بود. سوخت مصرفی این دستگاه تنها چند گرم هیدروژن معمولی است انرژی تولیدی از یک دستگاه شتاب دهنده یک گیگا الکترون ولت (Gev) برابر است با انرژی حاصل از سوختن ۰۰۰/۵۰۰/۲ لیتر بنزین خواهد بود. بنابراین اگر به مدت یک سال کار کند معادل انرژی ۵۰۰ میلیارد بشکه نفت انرژی تولید می کند.

ارزش اقتصادی این مقدار انرژی که ۲ برابر انرژی ذخایر نفت عربستان سعودی است با احتساب قیمت هر بشکه نفت بر مبنای ۲۰ دلار برابر است با ۱۰ تریلیون دلار. در صورتی که ما از این سیستم شتاب دهنده استفاده کنیم نیازی به سوزاندن این حجم عظیم نفت و گاز برای تولید انرژی نداریم. مزایای این سیستم عبارتند از:

1. می توان در ابعاد و اندازه های مختلف ساخت.
2. هزینه ساخت و نگهداری آن کم بوده است.
3. هیچ گونه زباله یا آلودگی محیطی تولید نمی کند. محصول نهایی آن آب خالص یا بخار آب است.
4. با استفاده از این دستگاه عملاً عمر منابع انرژی نامحدود می شود و منبع عظیمی از انرژی در دسترس خواهد بود.

در حوزه ذرات

1. الکترون ولت: واحد انرژی است و برابر انرژی یک الکترون یا پروتون وقتی از اختلاف پتانسیل یک ولت عبور کند برابر است با ۱۹-۱۰*۶/۱ ژول
   
2. یک گرم هیدروژن ۱۰۲۳ * ۰۲/۶ اتم بوده که به آن یک اتم گرم یا یک مول هیدروژن گویند.
   

اگر این مقدار هیدروژن از شتاب دهنده یک (Gev) عبور کند معادل انرژی آن برابر خواهد بود:

ژول ۱۰۱۳*۶/۹=۱۰۹*۱*۱۰۲۳*۰۲/۶* ۱۹-۱۰*۶/۱

یک کیلووات ساعت برابر است با ۰۰۰/۶۰۰/۳ ژول. بنابراین انرژی آن برابر است با ۲۶ کیلووات ساعت.

۱۰۱۳ *۶/۹ ژول تقسیم بر ۰۰۰/۶۰۰/۳ مساوی ۱۰۵*26

ماشین های شتاب دهنده

دید کلی:

ماشین های شتاب دهنده در انواع مختلف ساخته شده برای نمونه کاربردهایی از شتابدهنده های الکترونی را مطرح می کنیم . اشعه ایکس با نفوذ ، حاصل از این شتاب دهنده ها در معالجات بیماریها بکار برده شده و می شود. با بالا رفتن از انرژی اندرکنش تغییرات ذرات باریکه با هسته ها، موارد مهمی مطرح می شود و الکترونها در تمامی جهات پراکنده می شود.

• توزیع زاویه ای ذرات توسط آشکارسازها مورد مطالعه قرار می گیرد.
  
  
• در انرژیهای بالای 200MeV این امر روش قدرتمندی برای دریافت اطلاعات در مورد شعاعهای هسته ای و توزیع پروتونها در داخل هسته است.

• حتی در انرژیهای بالاتر حدود 600MeV نه تنها این الکترونهای شتاب یافته می توانند ساختار هسته را مشخص نمایند بلکه ساختار پروتونها و الکترونهای منفرد و مجزا را نیز می توانند کشف نمایند.

• به عنوان مثال به وسیله همین مطالعات یعنی ارسال کاوه های الکترونی (پوپ) به اطراف یک نوترون معلوم شده است :
  که نوترون بدون بار نیست بلکه دارای یک توزیع بار مثبت منفی است که میانگین آنها صفر است و حتی در مورد آن با محاسبات فرم فاکتور گشتاور مغناطیسی نیز پیدا شده است.

• هنگامی که ستون تابش شتابدار متشکل از ذرات سوای الکترونها پروتونها ، نوترونها و غیره) باشند وضعیت به طور اساسی فرق خواهد کرد. می دانیم که اینها هسته های اتمی اند و در نتیجه دارای بار مثبت می باشند به ترتیبی که توسط هسته های هدف طبق برهم کنش الکترومغناطیسی دفاع می شوند. ذره با عبور از هدف در اثر برخورد با الکترونهای اتمی به تدریج انرژی خود را از دست می دهد.

• دومین اختلاف بسیار اساسی این نوع باریکه ها ناشی از این حقیقت است که نیروهای بین هستک ها فقط الکترومغناطیسی نیستند. همان طور که می دانید این نتیجه گیری از ذرات وجودی هسته های اتمی ناشی می شود. در واقع اگر تنها نیروهای الکتریکی حاضر بودند، پروتونها همدیگر را دفع می کردند و هسته پایدار بجز هسته استثنایی هیدروژن نمی توانست وجود داشته باشد.

ارمغان ماشین های شتاب دهنده:

• نوع دیگری از نیروها که عموما نیروهای هسته ای نامیده می شوند وجود دارد که می بایست عهده دار نگهداری هسته در کنار همدیگر باشند.
• هنگامی که هسته های اتمی به عنوان پرتابه بکار روند، همین نیروهای هسته ای بر پراکندگی آنها اثر خواهند گذاشت در نتیجه اطلاعاتی درباره طبیعت آنها حاصل خواهد شد.

• طبیعت بنیادی نیروهای هسته ای دقیقا بیان نشده است. لیکن چندین واقعیت حتمی به هر صورت اساس قرار گرفته اند و به طور مثال شما می دانید که برد آنها بسیار کوتاه بودند ( از مرتبه ^13-10 سانتی متر).

• قدرت نیروهای هسته ای واقعا زیاد است. زیرا نیروی دافعه الکتروستاتیکی دو پروتون در چنین فاصله ای حدود 23 "کیلوگرم نیرو" است (به اندازه 1028 برابر وزن خودشان است). به سبب همین نیروها ، ماده هسته ای طوری فشرده شده است که چگالی d=3.5x10⁸gr/cm است.

• دو نوع نیرو داریم که بین دو هسته فرودی و هدف موثر است. نیروی الکتروستاتیکی که در فواصل طولانی موثر است و نیروهای هسته ای حاکم در فواصلی که دو ذره فوق العاده برهم نزدیک باشند.

توان ماشین های شتاب دهنده:

روشن است که نیروهای هسته ای بیشتر روی ذرات فرودی که به قدر کافی انرژی دارند که بتوانند بر سد الکتروستاتیکی حاصل از هدف غلبه کند، کنش نشان میدهد. از بین ماشین های شتابدهنده ذرات ، مولد الکترواستاتیک تک مرحله ای واندوگراف برای مثال با ماکزیمم انرژی 8MeV نمیتواند برای تولید اندرکنشها در هسته های هدف با عدد اتمی بیشتر از 28=Z بکار رود، حال آنکه یک سیکلوترون با 20MeV انرژی عملا دارای چنین محدویتی نیست. پس هر ماشین دارای گستره توانایی معین است.