برای اولین بار، نامساوی ِ مشهور ِ بل Bell در کوانتوم مکانیک، در یک آزمایش فیزیک انرژی زیاد آزموده شد. این نامساوی در آزمایش هایی با مزون های B در آزمایشگاه کـِک KEK ِ ژاپن، تا حد سه انحراف معیار نقض شد و ضمنا این آزمایش ها باز هم پیش بینی های کوانتوم مکانیک را تأیید کردند. قبلا بیشتر آزمایشهای مربوط به نامساوی بل با فوتون ها یا یون ها انجام می شدند. در آزمون های نامساوی بل، ویژگی های زوج ذره هایی را می سنجند که فاصله شان، از نظر نسبیت خاص، فضاگونه است: یعنی طی آزمایش، زمان کافی برای این که نور از یکی به دیگری برسد نیست. مثلا در یک آزمایش نوعی نامساوی بل، قطبش یک زوج فوتون را بر حسب زاویه محورهای قطبیگرها نسبت به هم می سنجند. کوانتوم مکانیک پیش بینی می کند بین ذره ها هم بستگی های ناموضعی هم می تواند باشد. این یعنی اگر یک فوتون مثلا در جهت عمودی قطبیده شده باشد، فوتون دیگر زوج آن حتما در جهت افقی قطبیده است، حال فاصله ی دو فوتون هر چه می خواهد باشد. اما بعضی از فیزیک پیشه ها معتقدند این نمی تواند درست باشد، و ذره های کوانتومی باید کمیت های موضعی یی (به اسم ِ متغیرهای نهانی) داشته باشند، که نمی توانیم بسنجیم شان. بل و دیگران نشان دادند با نوعی آزمایش که پارامتری به اسم S را می سنجد، می شود بین کوانتوم مکانیک و این نظریه های متغیرهای نهانی فرق گذاشت. به بیان ساده، نظریه های موضعی پیش بینی می کنند S همواره کوچکتر از دو است، در حالیکه پیش بینی کوانتوم مکانیک S=sqr(2)*2 است. وقتی S بزرگتر از 2 می شود، می گویند نامساوی بل نقض شده است. آپولو گو Apollo Go از دانشگاه مرکزی ملی تایوان و همکارانش در گروه بـِله Belle این آزمایش را در کارخانه ی B ی کـِک انجام دادند. در این شتابدهنده باریکه های الکترون و پوزیترون با هم برخورد می کنند و ذرات B مزونها و پادذره هایشان را تولید می کنند که اینها هم به ذرات سبک دیگر وامی پاشند. روج مزونها مثل روج فوتون رفتار می کنند. اما گروه بله Belle، به جای تحلیل هم بستگی بین جهت های قطبش، هم بسته گی های ذره-پادذره را با روشی به اسم برچسب طعم گذاری بررسی کرد. گو Go و همکارانش حساب کردند S=2.725 و خطای این سنجش چنان است که نامساوی تا حد سه انحراف ِ معیار نقض می شود. گو به فیزیکس وب Physicsweb گفت: "اگر کوانتوم مکانیک یک توصیف بنیادی ِ طبیعت باشد، با هر عدد کوانتومی یی باید هم بستگیهای ناموضعی دیده شود. در این آزمایش عدد کوانتومی ذره-پادذره کمیت ی بسیار بنیادی در فیزیک ِ ذرات است، و شاید نتایج ِ حاصل پی آمدهایی هم در این زمینه داشته باشند. منتظر نظر ذره نظریه پردازهای دیگرم." این گروه بنا دارد هم بستگی های ذره-پادذره را با جزئیات بیشتری بررسی کند و مرز بین مکانیک کلاسیک و کوانتوم مکانیک را بکاود.

اطلاعات اولیه

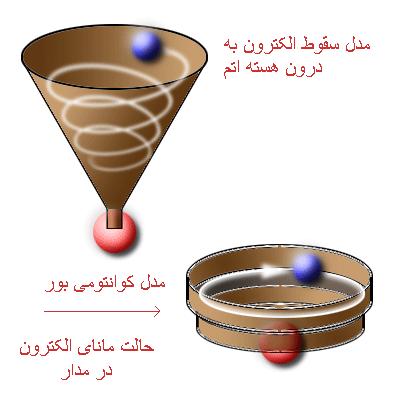در بررسی ساختار اتم مدلهای مختلفی ارائه شده است. ابتدایی‌ترین این مدلها ، مدل سیاره‌ای رادرفورد است. بعد از مدل سیاره‌ای رادرفورد ، نیلز بوهر مدل جدیدی را ارائه داد (مدل اتمی بوهر). این مدل می‌‌توانست ساختار طیفی اتم هیدروژن را توضیح دهد. در اصل موضوع بوهر که اساس و مبنای مدل بوهر است، فرض می‌‌شود که الکترونها مقیدند در مدارهایی حرکت کنند که در آنها اندازه حرکت الکترون مضرب درستی از h/2π باشد که h ثابت پلانک است. همچنین در این مدل فرض می‌‌شود که ترازهای انرژی کوانتیده‌اند. بعدها که ساختار طیف مربوط به عناصر مختلف مورد توجه قرار گرفت، انرژی هر الکترون در اتم با یک سری اعداد که به عنوان اعداد کوانتومی معروف هستند، مشخص کردند.

اعداد کوانتومی اصلی

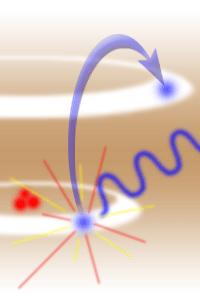
گفتیم که ترازهای انرژی در اتم گسسته هستند. این امر به این معنی است که اگر اتم توسط تابش الکترومغناطیسی بمباران شود، تابش توسط الکترونها جذب می‌‌شود. لذا الکترونها از ترازهای اولیه یا پایه خود تحریک شده و به ترازهای برانگیخته می‌‌روند، اما چون این حالت یک حالت ناپایدار است، لذا الکترون با گسیل تابش از تراز برانگیخته به تراز اولیه خود برمی‌‌گردد. مقدار انرژی جذب شده یا گسیل شده متناسب با فاصله ترازهای انرژی است، یعنی اگر انرژی تراز اولیه را با E و انرژی تراز برانگیخته را با ΄E مشخص کنیم، در این صورت فرکانس نور گسیل شده یا تحریک شده از رابطه E - E΄ = hv حاصل می‌‌شود.

از طرف دیگر ، چون طبق اصل موضوع بوهر ، اندازه حرکت الکترون باید مضرب صحیحی از h/2π باشد، بنابراین اگر با تقریب مدار حرکت الکترون به دور هسته را دایره‌ای به شعاع r فرض کنیم، در این صورت nh/2π خواهد بود که در این رابطه v سرعت الکترون و m جرم آن است. همچنین با توجه به این که نیروی وارد شده از طرف هسته بر الکترون نیروی مرکزی است، لذا اگر بار هسته را برابر ze بگیریم که در آن z عدد اتمی است، مقدار نیروی وارد بر الکترون برابر ze²/r² = mv²/r خواهد بود. از ترکیب این روابط می‌‌توان مقدار انرژی الکترون در هر تراز اتمی را بدست آورد.

در این صورت انرژی از رابطه: E = 1/2mc²/(zα)² بدست می‌آید که در این رابطه α مقدار ثابتی است که برابر α = 1/137 e²/ћc بوده و ثابت ساختار ریز نامیده می‌‌شود. مقدار n که در رابطه انرژی ظاهر شده است، عدد کوانتومی اصلی نامیده می‌‌شود. البته می‌‌توان مقدار انرژی الکترون در هر تراز را از حل معادله شرودینگر محاسبه کرد. در این صورت نیز رابطه انرژی الکترون در هر تراز برحسب یک عدد کوانتومی که به عدد کوانتومی اصلی معروف است، مشخص می‌‌شود.

عدد کوانتومی اندازه حرکت زاویه‌ای مداری

نظریه اتم تک الکترونی بوهر عدد کوانتومی اصلی n را معرفی می‌‌کند که مقدار درست آن انرژی کل اتم را مشخص می‌‌کند. عدد کوانتومی n که یک عدد صحیح و مثبت است، بزرگی اندازه حرکت زاویه‌ای الکترون به دور هسته را بر اساس اصل موضوع بوهر ، طبق رابطه L = nћ مشخص می‌‌کند. ћ عدد ثابتی است که بصورت نسبت ثابت پلانک بر عدد 2π تعریف می‌‌شود، اما از دیدگاه مکانیک موجی درست نیست که برای الکترون یک مسیر مشخص دایره‌ای یا شکل دیگری را در نظر بگیریم. (اصل عدم قطعیت مانع این کار است) و نیز از این دیدگاه قاعده بوهر در مورد کوانتش بزرگی اندازه حرکت زاویه‌ای درست نیست.

بر خلاف نظریه کلاسیک ، مکانیک موجی نشان می‌‌دهد که بزرگی اندازه حرکت زاویه‌ای مداری (L) یک دستگاه اتمی کوانتیده است و مقادیر ممکن آن می‌‌تواند از رابطه: L = (l(l + 1))^1/2ћ بدست آید. در این رابطه l عدد صحیحی است که عدد کوانتومی ‌اندازه حرکت زاویه‌ای مداری نامیده می‌‌شود. برای مقدار مفروض از عدد کوانتومی ‌اصلی n ، مقادیر ممکن l ، اعداد درست از صفر تا n - 1 خواهد بود. به عنوان مثال ، اگر n = 2 باشد، در این صورت l می‌‌تواند مقادیر (1,0) را اختیار کند.

در نمادگذاری ترازها هر مقدار از l با یک حرف مشخص می‌‌شود. در این نمادگذاری مقدار l = 0 با حرف S و l = 1 با حرف l = 2 ، P با حرف D و ... مشخص می‌‌شود. چون انرژی فقط برحسب عدد کوانتومی ‌اصلی مشخص می‌‌شود، بنابراین در مورد تک الکترونی که تحت تأثیر یک نیروی کولنی از جانب هسته است و در تراز n = 3 قرار دارد، هر سه حالت l = 0 , 1 , 2 دارای انرژی یکسانی خواهند بود.

اعداد کوانتومی ‌مغناطیسی مداری

گفتیم که الکترون در اثر نیرویی که از طرف هسته بر آن وارد می‌‌شود، حول هسته می‌‌چرخد. چون الکترون یک ذره باردار است، بنابراین مدار الکترون را می‌‌توان یک مدار مغناطیسی در نظر گرفت. برای این مدار مغناطیسی و در واقع برای الکترون می‌‌توان یک گشتاور دو قطبی مغناطیسی تعریف نمود. این کمیت بر اساس اندازه حرکت زاویه‌ای مداری الکترون تعریف می‌‌شود. یعنی از رابطه μ = eL/2m حاصل می‌‌شود که در آن μ گشتاور دو قطبی مغناطیسی است.

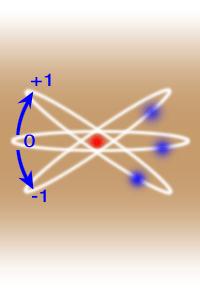
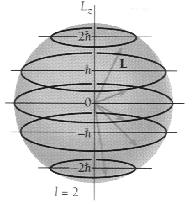
حال اگر یک میدان مغناطیسی خارجی اعمال شود، در این صورت میدان سعی می‌‌کند تا گشتاور دو قطبی مغناطیسی و به تبع آن L را در راستای میدان قرار دهد، اما در مکانیک موجی بردار اندازه حرکت زاویه‌ای مداری L نمی‌‌تواند هر جهتی را نسبت به میدان مغناطیسی اختیار کند، بلکه محدود به جهتهای به خصوصی است که برای آن مؤلفه بردار اندازه حرکت زاویه مداری ، در راستای میدان مغناطیسی ، مضرب دستی از ћ باشد. بنابراین اگر جهت میدان مغناطیسی را در راستای محور z اختیار کنیم، در این صورت مؤلفه z بردار L از رابطه L_z = m_l ћ حاصل می‌‌شود. در این رابطه m_l عدد کوانتومی ‌مغناطیسی مداری است. به ازای یک مقدار مفروض l ، m_l می‌‌تواند مقادیر زیر را اختیار کند:

{m_l ={ l , l - 1 , l - 2 , … , 0 , … , - l

عدد کوانتومی ‌مغناطیسی اسپینی

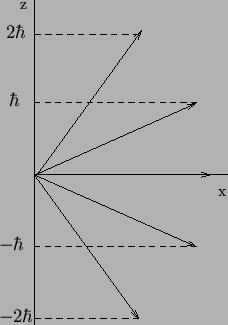در نظریه کوانتومی ‌سه ثابت فیزیک کلاسیک مربوط به حرکت ذره‌ای که تحت تأثیر جاذبه عکس مجذوری قرار دارد، کوانتیده‌اند. این سه ثابت عبارتند از: انرژی ، بزرگی اندازه حرکت زاویه‌ای مداری ، مؤلفه اندازه حرکت زاویه‌ای مداری در یک جهت ثابت از فضا. در مکانیک کوانتومی ‌به این ثابتهای حرکت اعداد کوانتومی n و l و m_l نسبت داده می‌‌شوند، اما علاوه بر این سه عدد کوانتومی ، عدد کوانتومی ‌دیگری به نام عدد کوانتومی ‌اسپینی که به مفهوم اسپین الکترون مربوط است، معرفی می‌‌شود.

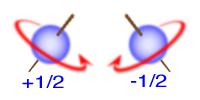
در سال 1925/1304 گود اسمیت و اوهلن یک اظهار داشتند که یک اندازه حرکت زاویه‌ای ذاتی ، کاملا مستقل از اندازه حرکت زاویه‌ای مداری ، به هر الکترون وابسته است. این اندازه حرکت ذاتی ، اسپین الکترون نامیده می‌‌شود. چون می‌‌توان آن را با اندازه حرکت ذاتی که هر جسم گسترده بر اساس دوران یا اسپین حول مرکز جرم خود دارد، مانسته داشت. البته لازم به توضیح است که در مکانیک موجی تلقی الکترون به عنوان یک کره ساده با بار الکتریکی صحیح نیست، بلکه صرفا به خاطر مشخص کردن اندازه حرکت زاویه‌ای اسپینی الکترون به کمک مدل قابل تجسم ، بهتر است که آن را به عنوان جسمی که در فضا دارای گسترش است و بطور پیوسته حول یک محور به دور خود می‌‌چرخد، فرض کنیم.

مانند اندازه حرکت زاویه‌ای مداری در اینجا نیز می‌‌توانیم یک گشتاور مغناطیسی مربوط به حرکت اسپینی الکترون در نظر بگیریم. چنانچه یک الکترون ، با گشتاور مغناطیسی دائمی خود ، در یک میدان مغناطیسی قرار گیرد، انتظار می‌‌رود که اسپین آن کوانتیده فضایی باشد، یعنی گشتاور مغناطیسی اسپینی و اندازه حرکت زاویه‌ای اسپینی به سمت گیری‌های خاصی محدود خواهند بود.

بنابراین اگر میدان مغناطیسی در راستای محور z فرض شود، در این صورت مؤلفه اندازه حرکت زاویه‌ای اسپینی L_sz در جهت این میدان از رابطه L_sz = m_sћ حاصل خواهد شد. در این رابطه m_s عدد کوانتومی ‌مغناطیسی اسپینی نامیده می‌‌شود. از آنجا که الکترون از دسته فرمیونها می‌‌باشد، بنابراین دارای اسپین نیم فرد خواهد بود، لذا عدد کوانتومی m_s فقط می‌‌تواند دو مقدار ممکن 2/1+ و 2/1- را اختیار کند.

 نمونه های اولیة رایانه های کوانتومی که از ذرات اتمی و زیر اتمی برای انجام محاسبات خود استفاده می کنند، عجایب آزمایشگاهی هستند و با شلیک طیف خاصی از لیزر به درون کریستالهای خاص، به آزمایش مایع درون دستگاه تولید MRI پزشکی می پردازند.

رایانه های کوانتومی می توانند در حل مسائل بزرگی مانند شکستن کدهای رمزی به صورت اعجاب انگیزی سریع باشند. امــا این نوع رایانه ها عمدتا در حد تئـوری باقی مانده اند. به همین دلیل پژوهشگران روش های مختلفی را آزمایش می کنند تا ببینند که آیا امکان ساخت آنها هست یا خیر.

پژوهشگران دانشگاه استانفورد و دانشگاه کیو(Kieo )در ژاپن، در تلاش برای ساخت وسایل کوانتومی کاملاً مشابه با رایانه های معمولی و کلاسیک هستند. این تیم با هدف ساختن رایانه های کوانتومی، به طور کامل از مواد متعارف مورد استفاده در رایانه ها- سیلیکون- استفاده می کنند.

تادیوس لاد، یکی از پژوهشگران دانشگاه استانفورد گفت:"" طراحیهــای مبتنی بر سیلیکون بســــیار شگفت انگیزند، زیرا همة مهندسین در طی بیش از 40 سال گذشته، فناوری سیلیکون را دنبال کرده اند.،،

رایانه های کوانتومی برای نشان دادن بیت های اطلاعاتی، ذرات اتمی یا زیر اتمی کیوبیتها را به کار می برند. هستة هر اتم می نواند همانند یک آهنربای کوچک عمل کند، و بسته به اینکه میدان مغناطیسی در چه جهتی قرار گیرد، صفر یا یک را نشان می دهد. رایانه های موجود، از وجود یا عدم وجود جریان الکـتـریـکـی حـاصـل از تـرانزیــستــورهـا برای نشان دادن یک ها و صفرهای اطلاعات دیجیتالی استفاده می کنند. هنگامی که یک اتم از محیطش جدا می شود، هسته در حالت کوانتومی غیر طبیعی ابر موقعیت ((Super Position قرار می گیرد. بــدین مـعنـی کـــه در آمیزه ای از تمام شرایط ممکن قرار می گیرد. یک کیوبیت در حالت ابــر موقـعـیـت مخلوطی از 1 و 0 است، و رشته ای از کیوبیت ها در حالت ابر موقعیت می تواند هر ترکیبی از یک ها و صفرها را به طور همزمان نشان دهد.

قدرت یک رایانه کوانتومی ناشی از توانایی آن برای کنترل و ارائة همزمان ترکیبات عددی مختلف جهت دستیابی بـه کـدهای رمــز است. در صورتی که رایانـه های فـعلـی در هر زمان فقط یک پاسخ را کنترل می کنند. لذا یک رایانه کوانتومی کار بسیاری از رایانه ها را انجام می دهد.

پـــژوهشگــران در بــزرگتـرین نــمــونــه رایـانـه کـوانـتــومی کـه تا کنون ساخته شده، از فناوری رزونانس مغناطیس هسته ای ( NMR ) مایع برای دستکاری هفت کیوبیت استفاده کردند. NMR که دارای فناوری ورای دستگاه های تصویربرداری رزونانس مغناطیسی (MRI ) است از میدان های مغناطیسی و امواج رادیویی برای تغییر و اندازه گیری هسته های اتمی در مولکول های تشکیل دهندة مایع استفاده می کند. با این وجود، پژوهشگران عموماً معـتقدند کـه رایـانــه های کوانتومی NMR مایع نمی توانند بزرگتر از 10 کیوبیت ساخته شوند، زیرا قدرت سیگنال های رادیویی حاصل از کیوبیت ها در مـقـایـسـه بـا سیگنـال ناخواستة هر کیوبیت اضافی، به صورت تصاعدی کاهش می یابد. یک رایانــه کـوانــتـومـی بــرای استفاده از تـوانایی های عظیم خود باید شامل هزاران یا میلیون ها کیوبیت باشد. رایانه های کلاسیک امروزی شامل میلیون ها ترانزیستور هستند.

طرح پژوهشگران دانشگاه های استانفورد و کیو از فناوری NMR نیز استفاده می کند، اما به شکل جامد. طرح آنها به این صورت است که به جای اتم های سیلیکون از ایزوتوپ سیلیکون 29 استفاده کنند، زیرا در سیلیکون 29 هسته ها همانند آهنربا عمل می کنند در حالی کــه سیلیکون مـعمـولی چنیـــن نیست. هسته های ایزوتوپ سیلیکون 29 مشکل سیگنال های ناخواسته را کاهش می دهد. چالش دیگری که در ساخت رایانه های کوانتومی وجود دارد، حفاظت کیوبیت ها از شرایط شکننده است. انرژی محیط اطراف می تواند کیوبیت ها را نابسامان کند و باعث تفرق(Decoherence) آنها شود. لاد گفت که تفرق شبـیــه حالتی است کـــه یـک رأس در حال گردش ( Spinning Top) از بین رفته یا آسیب می بیند. کیوبیتی که به مدت طولانی تری منسجم باقی بماند، باعث می شود که رایانه کوانتومی عملیات بیشتری را انجام دهد. طرح سیلیکون جایگزین شده، مسأله عدم انسجام و تفرق و همچنین محافظت از هسته های مغناطیسی را مـورد توجه قرار می دهد و باعث پایدار شدن شرایط کوانتومی می شود.

طرح این پــژوهشگــران نیازمند بــه کارگیــری رشته ای از هسته های سیلیکون 29 برای تشکیل یک کیوبیت است. لاد می گوید: "" اگر ویفرهای سیلیکونی موجود شکسته شوند ساختار کریستالی لبه ها، پله هایی را تشکیل می دهد و اتم های سیلیکون 29 بر روی این لبــه ها نشستــه و بـه گـوشــه هـای این پله ها حرکت می کنند و زنجیره هایی را ایجاد می کند. اندازه گیری جهت مغناطیسی زنجیره های حاوی فقط چند صد هستــة اتمی در مقایسه با گروههایی شامل میلیاردها هستة اتمی در مولکولهای مایع کار مشکلی است، بطوریکه چنین خاصیت مغناطیسی تا کنون اندازه گیری نشده است.،،

این پژوهشگران برای اندازه گیری و کنترل این زنجیره های کیوبیتی، آنها را در میدان های مغناطیسی با قدرتهای مختلف قرار می دهند و هر زنجیر به فرکانس رادیویی متفاوتی پاسخ می دهد. یعنی اصولاً هر کیوبیت، کانال رادیویی مخصوص به خود دارد. لذا با تنظیم فـرکانس امــواج رادیـویی با یک آنتن می تـوان آن را برای هر هسته تنظیم کرد. این سیگنال های فرکانس رادیویی می توانند هسته ها را به هر طریق که ما بخواهیم بچرخانند.

این رایانه های کوانتومی عملیات های منطقی را از طریق مراحل پیچیدة چرخش انجام می دهند. این طرح، او لین طــرح پـیـشنهـاد شده برای ساخت رایانه های کوانتومی از سیلیکون نیست. بروس کان، پژوهشگر دانشگاه مریلند، طرحی را برای ساخت کیوبیت ها از اتم های فسفر که در فواصل معینی از یک تراشه سیلیکونی گنجانده شده اند ابداع کرده است. لاد گفت، کیوبیت های این طرح از نظر تفرق مشکل کمتری دارند و احتمالاً حتی برای خواندن اطلاعات نیز از همة روش های سیلیکونی که پژوهشگران به کار می برند مناسبتر باشند.

بنا بر اظهار نظر لاد، در دراز مدت ممکن است که طرح کا ن دارای آیندة بهتری باشد، زیرا این احتمال بیشتر وجود دارد که برای ساخت رایانه های کوانتومی قابل استفاده، نیاز به تولید دستگاه هایی شود که دارای هزاران یا میلیون ها کیوبیت هستند. تفاوت عمده در آن است که رایانه های ما در مدت کوتاه تری قابل حصول و واقع بینانه تر هستند، در حالی که رایانه های کان از دسترس دورتر و بنابراین غیر متحمل تر هستند.

بنا به اظهارات لاد، طرح پژوهشگران دانشگاه های استانفورد و کیو جالب توجه است و شاید عملی ساختن آن از انواع دیگر رایانه های کوانتوم سیلیکونی آسان تر باشد. اما استفاده از تعداد زیادی کیوبیت در آن مقدور نیست.

ایلی یابلونویچ، استاد مهندسی الکترونیک دانشگاه کالیفرنیا، لوس آنجلس می گوید: که کار این پژوهشگران ممکن است برخی از مسائل رایانه های مــوجـود را حـل کند. وی گفت که به کارگیری رشتــه هایی از هسته های سیلیکونی ممکن است نسبت به استفاده از مایعات، دارای برتری های زیادی باشد.

با وجـود این، سـرعـت ایـن فـنـاوری کـمـتر از یک کیلو هرتز در ساعت باقی می ماند. مـیـدان هـای مـغـنـاطیــسـی بـاعـث رزونـانس هسته های اتـمی در فــرکــانس هـای نسبتاً پایـیـن و کـاهش ســرعت انـــجـام فرامــین می شوند. سیگنال های رادیــویـی کــه بـرای کنـتـرل کیوبیت ها به کار برده شده اند باید با فرکانس رزونانس پایین آنها هماهنگ شوند.

بــه همین خاطر، دیگر تیم های پژوهشی به جای کار با هسته های اتمی در حال کار با الکـتـرون هـا هستند. یابلونویچ می گوید: این نوع از رایانه های کوانتومی سیلیکونی بسیاری از مـزایای رایانــه های نوع دیگر را داشته و عـلاوه بـر آن دارای سرعت یک گیگاهرتز در ساعت هستند. الکترون ها نیز همانند هسته ها مانند آهنرباهای کوچکی عمل می کنند اما آنها را می توان با پالس های فوق سریع نور لیزر دستکاری کرد. مانعی کــه بـرای بـه کارگیری الکترون ها وجود دارد این است که شرایط کوانتومی آنها در مقایسه با شرایط کوانتومی دوام کمتری دارد.

لاد می گوید: کـــه تخمین این کــه توسعـة کامل رایانه های کـوانــتــومی تــا چـه مدت زمـانــی به طــول خـواهد انـجـامـیـد مشکل است اما با یک حساب سرانگشتی، این امر احتمالاً در طی 20 سال آینده میسر خواهد شد.

نوشته : آقای دکتر نادر ریاحی عالم، عضو هیئت علمی دانشگاه علوم پزشکی تهران, گروه فیزیک پزشکی

 مقدمه

هنگامیکه اروپا در ظلمت جهل و بی خبری بسر می برد، دانشمندان اسلامی و در راس آنان اندیشمندان ایرانی اندوخته های علمی یونانیان را جمع آوری و حراست کردند و با دانش و اندیشه های ایرانیان باستان درآمیختند. تعاریف و اصول هندسه ی اقلیدسی توسط ایرانیان مورد بررسی و نقد قرار گرفت. مثلثات کروی توسط فضلای ایرانی ابداع و دستگاه اعداد با کشفیات هندیان تکمیل و بوسیله ی بازرگانان به اروپا برده شد. از قرن یازدهم میلادی به بعد بعضی از کشیشان به جامه ی طلاب مسلمان در می آمدند و کتبی را که با دقت محافظت می شد با خود به غرب می بردند و ترجمه می کردند.

در قرن شانزدهم دستگاه خورشید مرکزی منظومه شمسی تدوین و مسیر حرکت سیارات با دقت رصد شد. در نتیجه تقدس دایره ها در هم شکسته شد و مدار بیضوی حرکت سیارات مورد قبول واقع شد. روش استقرایی توانی نو یافت و به مقابله با قیاس برخاست و مسیر جدیدی برای اندیشه های علمی بوجود آمد.

آزمایش کردن قباحت خود را از دست داد و اجسام از بلندی رها شدند تا زمان سقوط آنها بطور تجربی بررسی شود. قوانین سقوط آزاد اجسام به کل جهان تعمیم داده شد شد و قانون جهانی گرانش کشف گردید. علت حرکت سیارات به دور خورشید صورت بندی شد. اختراع و تکمیل تلسکوپ انسان را با دنیایی رو به رو ساخت که قبل از آن هرگز تصورش نمی رفت. آنگاه ناچیزی زمین در مقابل کاینات به اثبات رسید.

استفاده از نماد گرایی در ریاضیات آغاز و هندسه تحلیلی به عنوان ابزاری قدرتمند برای تجسم و تکمیل کشفیات حساب دیفرانسیل و انتگرال به کار گرفته شد. ماهیت فیزیکی نور با آزمایش مورد سئوال قرار گرفت. در نتیجه نظریه ی دانه ای و نظریه ی موجی بودن نور برای توجیه آن ابداع شد. عنصر پنجم ارسطوئی اتر بیش از پیش بکار گرفته شد. اما این بار نه به عنوان یک عنصر، بلکه به عنوان زمینه ای برای انتشار نور و توجیه حرکت نور در فضا و انتقال نیروی گرانش و تصور می شد که کالبد فضا از اتر انباشته شده است.

1-2

عصر تاریکی و دوره ی انتقال اول

با سقوط امپراطوری روم در اواسط قرن پنجم میلادی تمدن در اروپای غربی به سطح بسیار پائینی رسید. تعلیم و تربیت تقریباً از بین رفت و تنها راهبان دیرهای کاتولیک و معدودی افراد غیر روحانی با فرهنگ و دانش یونانی و لاتینی رشته ی باریکی داشتند.

در این دوران دانش باستان توسط دانشمندان اسلامی محفوظ ماند، دانشمندان اسلامی ضمن آنکه دانش یونانی را حفظ کردند، اندوخته های علمی ایران باستان، چین و هند را را نیز جمع آوری نموده، خود نیز به باروری آن کوشیدند. خلفای بغداد به حامیان علم بدل گشتند و فضلای برجسته ای را به دربار خود فراخواندند. آثار هندی و یونانی از جمله آثار برهمگویت، و اصول اقلیدسی و مجسطی به عربی ترجمه شد. کتب یونانی به عنوان یکی از شرایط صلح، از امپراطور بیزانس مصادره شد و در اختیار فضلای عرب زبان قرار گرفت. در این عصر فضلای زیادی به نوشتن آثاری در زمینه ریاضیات و نجوم پرداختند که مشهورترین آنها محمد ابن موسی الخوارزمی بود. خوارزمی رساله ای در جبر و کتابی در باره ارقام هندی نوشت که بعدها در قرن دوازدهم به لاتین ترجمه شد و تاثیر زیادی در اروپا گذاشت. ابوالوفا بوزجانی کتب بطلمیوس را ترجمه و تشزیح کرد و شرحی بر کتاب دیوفانتس نوشت. اصیل ترین و بدیع ترین اثر جبری حل معادله درجه سوم توسط خیام بوجود آمد. وی اصلاحیه دقیقی نیز برای تقویم انجام داد.

خواجه نصیرالدین طوسی اولین اثر در باب مثلثات مسطحه و کروی را نوشت و کار پیشتر خیام را با شرح و تصیحیحاتی منتشر کرد که ساکری کارش را در هندسه نااقلیدسی با یاد داشتی از نوشته های نصیرالدین در باب توازی شروع کرد. نوشته های خواجه نصیرالدین توسط جان والیس در آکسفورد تدریس شد.

ابن هیثم که در غرب به الهازن شناخته می شود، بزرگترین فیزیکدان مسلمان شناخته شده است. وی رساله ای در نور نوشت و ذره بین را کشف کرد. به نسبت زاویه تابش و زاویه انکسار پی برد و اصول تاریکخانه را شرح داد و در مورد قسمتهای مختلف چشم بحث کرد. رساله ی نور ابن هیثم نفوذ زیادی در اروپا گذاشت. کارهای وی توسط کمال الدین فارسی پیگیری شد.

در مورد نجوم تنها کافیست گفته شود که بسیاری از نامها و واژه های امروزی در نجوم ریشه عربی دارند. بتدریج آثار علمی ایرانیان تنها زینت بخش کتاب خانه گردید و هنگامیکه شرق در حال به خواب رفتن علمی و غفلت بود، غرب در حال بیدار شدن بود. اوضاع علمی سایر کشورهای اسلامی و هندوستان و چین هم از ایران بهتر نبود، بلکه بدتر بود.

2-2

فیزیک در ایران

کشور ما نسبت دیرینه ای در نجوم دارد. قدیمی ترین متن ایران پیش از اسلام، اوستا کتاب دینی زرتشتیان است که متاسفانه فقط یک پنجم آن باقی مانده است. در این متن به کروی بودن زمین اشاره شده است که این یک ردپای نجومی از ایران باستان است. همچنین در متن های دینی زرتشتی مربوط به دوره ساسانی به نام صورت های فلکی، ستاره ها و سیارات اشاره شده است.

مورد دیگر نجوم ایران پیش از اسلام مربوط به قرن اول میلادی یعنی 6 قرن پیش از ظهور اسلام است.در قرن اول میلادی عده ای از فعالان (رهبران دینی که هم رهبر بودن و هم دانشمند) به علتی نامعلوم و زمان اشکانیان از سیستان به هند مهاجرت کردند و دانش و فرهنگ ایرانی را با خود به این کشور بردند و آن را با فرهنگ و دانش هندی آمیخته کردند. گفته می شود این افراد همچنین در هند باقی مانده اند و تمایز نژادی خود را حفظ کرده اند. در هر حال این مسلم است که تقویم ایرانی که این افراد به هند بردند که در آن شروع سال اول بهار است و هنوز در هند مورد استفاده قرار می گیرد. البته آنها عملا از تقویم اروپایی استفاده می کنند اما تقویم رسمی در قانون اساسی این کشور همان تقویم ایرانی است. از کتب قدیمی ایران کتاب نجومی باقی نمانده است غیر یک اثر مهم به نام ذیج شهریاران. ذیج به معنی کتابچه نجومی است که لغت قدیمی فارسی است. این کتاب در زمان بهرام گور و توسط پادشاهان ساسانی تالیف شده است که یک قرن بعد در زمان انوشیروان تصمیم گرفتند این کتاب را کامل تر کنند که به دستور انوشیروان کتاب های نجوم یونان و هند خوانده شد و مقایسه کردند و گفتندکه کتاب های نجوم هندی دقیق تر است در نتیجه یک ویرایش جدیدی از ذیج شهریار براساس متن های هندی فراهم کردند. بعضی از منجمان اسلامی مثل ابوریحان بیرونی و خوارزمی مطالبی از این کتاب را در کتاب های خود آورده اند.

مثلا ابوریحان بیرونی کتابی به نام افراط المقال فی امر الضلال (مقاله ای یکتا در مورد سایه ها) دارد که در آن روش مدرج کردن ساعت های آفتابی را از کتاب ذیج شهریار نقل کرده است. همچنین در یکی از نوشته های دینی زرتشتی یک آیین مقدسی ذکر شده است که گفتند این آیین باید زمانی انجام شود که ماه، ستاره ها، سیاره ها و خورشید در یک موقعیت ویژه که در رسانه ذکر شده است، باشد. در عین حال، در نوشته هایی که به زبان پهلوی است برای محاسبه موقعیت ماه، خورشید، ستاره ها و سیاره ها گفته شده است که باید محاسبه آنها براساس یک ذیج (کتابچه نجومی) باشد و آنجایی که از منابع ساسانی نام برده از ذیج هندی، ذیج شهریاران و ذیج بطلمیوس نام برده است به این ترتیب مشخص می شود که در زمان ساسانیان، ایرانی ها با نجوم یونان باستان که خیلی پیشرفته بود آشنا بوده اند که شاخص تر اثر آن کتاب نجومی یونان باستان است که بعدها به عربی ترجمه شد. ولی این عقیده هم وجود دارد که اولین ترجمه آن از یک ترجمه فارسی قدیمی گرفته شده است. نجوم ایران باستان از نجوم دوره یونان باستان تاثیر گرفته و بر نجوم دوره اسلامی اثر گذاشت و نجوم این دوره هم بعدها بر تکامل نجوم در اروپا تاثیر گذاشت. بعد از اسلام یکی دو قرن صرف کشمکش و تثبیت حکومت جدید در ایران شد. در این دوره یا هیچ اثری بوجود نیامد و یا اگر به وجود آمد باقی نماند. اما بعد از آن از قرن سوم تا قرن 7 و 8 هجری شکوفایی بسیاری در کشورهای اسلامی به خصوص در ایران به وجود آمد و دانشمندان دستاوردهای زیادی به وجود آوردند که به دوره طلایی اسلامی شهرت یافت.

خیام غیاث الدین ابوالفتح، عمر بن ابراهیم خیام (خیامی) در سال 439 هجری (1048 میلادی) در شهر نیشابور و در زمانی به دنیا آمد که ترکان سلجوقی بر خراسان، ناحیه ای وسیع در شرق ایران، تسلط داشتند. وی در زادگاه خویش به آموختن علم پرداخت و نزد عالمان و استادان برجسته آن شهر از جمله امام موفق نیشابوری علوم زمانه خویش را فراگرفت و چنانکه گفته اند بسیار جوان بود که در فلسفه و ریاضیات تبحر یافت. خیام در سال 461 هجری به قصد سمرقند، نیشابور را ترک کرد و در آنجا تحت حمایت ابوطاهر عبدالرحمن بن احمد , قاضی القضات سمرقند اثر برجسته خود را در جبر تألیف کرد.

خیام سپس به اصفهان رفت و مدت 18 سال در آنجا اقامت گزید و با حمایت ملک شاه سلجوقی و وزیرش نظام الملک، به همراه جمعی از دانشمندان و ریاضیدانان معروف زمانه خود، در رصد خانه ای که به دستور ملکشاه تأسیس شده بود، به انجام تحقیقات نجومی پرداخت. حاصل این تحقیقات اصلاح تقویم رایج در آن زمان و تنظیم تقویم جلالی (لقب سلطان ملکشاه سلجوقی) بود.

در تقویم جلالی، سال شمسی تقریباً برابر با 365 روز و 5 ساعت و 48 دقیقه و 45 ثانیه است. سال دوازده ماه دارد 6 ماه نخست هر ماه 31 روز و 5 ماه بعد هر ماه 30 روز و ماه آخر 29 روز است. هر چهار سال، یکسال را کبیسه می خوانند که ماه آخر آن 30 روز است و آن سال 366 روز می شود در تقویم جلالی هر پنج هزار سال یک روز اختلاف زمان وجود دارد در صورتیکه در تقویم گریگوری هر ده هزار سال سه روز اشتباه دارد.

دستاوردهای علمی خیام برای جامعه بشری متعدد و بسیار درخور توجه بوده است. وی برای نخستین بار در تاریخ ریاضی به نحو تحسین برانگیزی معادله های درجه اول تا سوم را دسته بندی کرد، و سپس با استفاده از ترسیمات هندسی مبتنی بر مقاطع مخروطی توانست برای تمامی آنها راه حلی کلی ارائه کند. وی برای معادله های درجه دوم هم از راه حلی هندسی و هم از راه حل عددی استفاده کرد، اما برای معادلات درجه سوم تنها ترسیمات هندسی را به کار برد؛ و بدین ترتیب توانست برای اغلب آنها راه حلی بیابد و در مواردی امکان وجود دو جواب را بررسی کند. اشکال کار در این بود که به دلیل تعریف نشدن اعداد منفی در آن زمان، خیام به جوابهای منفی معادله توجه نمی کرد و به سادگی از کنار امکان وجود سه جواب برای معادله درجه سوم رد می شد. با این همه تقریبا چهار قرن قبل از دکارت توانست به یکی از مهمترین دستاوردهای بشری در تاریخ جبر بلکه علوم دست یابد و راه حلی را که دکارت بعدها (به صورت کاملتر) بیان کرد، پیش نهد.

خیام همچنین توانست با موفقیت تعریف عدد را به عنوان کمیتی پیوسته به دست دهد و در واقع برای نخستین بار عدد مثبت حقیقی را تعریف کند و سرانجام به این حکم برسد که هیچ کمیتی، مرکب از جزء های تقسیم ناپذیر نیست و از نظر ریاضی، می توان هر مقداری را به بی نهایت بخش تقسیم کرد. همچنین خیام ضمن جستجوی راهی برای اثبات "اصل توازی" (اصل پنجم مقاله اول اصول اقلیدس) در کتاب شرح اصول مشکل آفرین کتاب اقلیدس، مبتکر مفهوم عمیقی در هندسه شد. در تلاش برای اثبات این اصل، خیام گزاره هایی را بیان کرد که کاملا مطابق گزاره هایی بود که چند قرن بعد توسط والیس و ساکری ریاضیدانان اروپایی بیان شد و راه را برای ظهور هندسه های نااقلیدسی در قرن نوزدهم هموار کرد. بسیاری را عقیده بر این است که مثلث حسابی پاسکال را باید مثلث حسابی خیام نامید و برخی پا را از این هم فراتر گذاشتند و معتقدند، دو جمله ای نیوتن را باید دو جمله ای خیام نامید. البته گفته می شود بیشتر از این دستور نیوتن و قانون تشکیل ضریب بسط دو جمله ای را جمشید کاشانی و نصیرالدین توسی ضمن بررسی قانون های مربوط به ریشه گرفتن از عددها آورده اند.

استعداد شگرف خیام سبب شد که وی در زمینه های دیگری از دانش بشری نیز دستاوردهایی داشته باشد. از وی رساله های کوتاهی در زمینه هایی چون مکانیک، هیدرواستاتیک، هواشناسی، نظریه موسیقی و غیره نیز بر جای مانده است. اخیراً نیز تحقیقاتی در مورد فعالیت خیام در زمینه هندسه تزئینی انجام شده است که ارتباط او را با ساخت گنبد شمالی مسجد جامع اصفهان تأئید می کند.

اما گذشته از همه اینها، بیشترین شهرت خیام در طی دو قرن اخیر در جهان به دلیل رباعیات اوست که نخستین بار توسط فیتزجرالد به انگلیسی ترجمه و در دسترس جهانیان قرار گرفت و نام او را در ردیف چهار شاعر بزرگ جهان یعنی هومر، شکسپیر، دانته و گوته قرار داد.

خواجه نصیرالدین محمد بن حسن جهرودی طوسی مشهور به خواجه نصیرالدین طوسی از اهالی جهرود از توابع قم بوده است که در تاریخ 15 جمادی الاول سال 597 هجری قمری ولادت یافته است. او به تحصیل دانش، علاقه زیادی داشت و از دوران جوانی در علوم ریاضی و نجوم و حکمت سرآمد شد و از دانشمندان معروف زمان خود گردید.

خواجه نصیرالدین طوسی ستاره درخشانی بود که در افق تاریک مغول درخشید و در هر شهری پا گذارد آنجا را به نور حکمت و دانش و اخلاق روشن ساخته و در آن دوره تاریک و در آن عصری که شمشیر تاتار و مغول خاندانهای کوچک و یا بزرگ را از هم پاشیده و جهانی از حملات مغولها به وحشت فرو رفته و همه در گوشه و کنار منزوی و یا فراری می شدند و بازار کسادی دانش و جوانمردی و مروت می بود و فساد حکمفرما. وجود و بروز چنین دانشمندی مایه اعجاب و اعجاز است.

تاسیس رصدخانه مراغه و انجام نخستین فعالیت علمی، پژوهشی و آموزشی در این موسسه از مهم ترین اقدامات این دانشمند است. رصدخانه مراغه به عنوان بزرگ ترین مرکز پژوهشی نجومی در زمان خود مطرح بوده است و امروز نیز علاوه بر ثبت در کتب، جزوات و اسناد ملی و بین المللی هر ساله صدها محقق نجوم در داخل و خارج از کشور را به خود جذب می کند.

همچنین خواجه نصیرالدین طوسی با انجام نخستین کار علمی و آموزشی در رصدخانه بین المللی مراغه پس از گذشت 750 سال از زمان فعالیت های علمی دراین مرکز پیشتاز نجوم در دنیای قدیم است. رصدخانه مراغه در سال 657 هجری قمری به دستور هلاکوخان و به همت دانشمند ایرانی خواجه نصیرالدین طوسی ساخته شد که ساخت آن 15 سال به طول انجامید. در این رصدخانه اسباب و آلات نجومی بسیاری متمرکز شده بود که متاسفانه این مجموعه بعد از سال 703 هجری قمری بر اثر زلزله و بی توجهی حکام رو به ویرانی گذاشت.

گفته می شود کتابخانه آن دارای چهار هزار جلد کتاب بوده است که از بغداد به این رصدخانه انتقال یافته بود. رصدخانه کهن مراغه بنابر اسناد معتبر الهام بخش تولد رصدخانه های سمرقند در تاجیکستان اوجین در هندوستان، فندو در بنارس اورانین برگ در دانمارک و رصدخانه شانگهای چین بوده است.

3-2

بیداری غرب و دوره ی انتقال دوم

ارتباط غربیان با جوامع اسلامی بویژه از طریق بازرگانان موجب توجه آنان آثار علمی اندیشمندان اسلامی شد. در این دوره مسیر برعکسی آغاز شد بدین ترتیب که چون بسیاری از آثار نجومی یونان باستان از بین رفته بود و فقط ترجمه عربی آن باقی مانده بود به لاتین ترجمه شدند. در این دوره بود که تعداد زیادی از اصطلاحات عربی به زبان های اروپایی راه پیدا کرد.

در حدود سال 950 میلادی ژربر متولد شد، وی در مدارس مسلمانان اسپانیا درس خواند و در مراجعت ارقام عدد نویسی عربی را با خود به اروپای مسیحی برد. ژربر مورد سوء ظن معاصرانش قرار گرفت و متهم شد که روح خود را به شیطان فروخته است. با این حال ژربر به تدریج در کلیسا ترقی کرد و سرانجام در سال 999 به مقام پاپی انتخاب شد. بدین ترتیب ورود آثار کلاسیک علوم یونانی و اسلامی به اروپای غربی شروع شد.

در حدود 1120 میلادی یک راهب انگلیسی به نام آدلارد باثی که در اسپانیا درس خوانده بود، خود را در جامه یک طلبه در آورد و به گنجی از دانش که شدیداً مورد حفاظت بود دست رسی پیدا کرد. وی اصول اقلیدس و جداول خاورزمی را به لاتین ترجمه کرد. قرن دوازدهم میلادی به قرن ترجمه آثار و فرهنگ و دانش اسلامی بدل گشت. کوشاترین مترجم این عصر گراردوی کرمونایی بود که بالغ بر 90 اثر عربی را به لاتین ترجمه کرد. مجسطی، اصول اقلیدس و جبر خوارزمی از آن جمله بودند.

در حدود سال 1250 میلادی، اکوایناس اساس استدلال و منطق ارسطو را بکار برد. وی بر اساس اصول ارسطویی سیستم تومیسم Tomism را بنیاد نهاد که در حال حاضر نیز پایه الهیات کلیسای کاتولیک رومی است. دیگران نیز به زودی از احیای اندیشه های یونانی در زمینه های دنیوی استفاده کردند. مهمترین کار در این زمینه با انتشار کتاب کوپرنیک صورت گرفت که در آن یکی از بدیهیات اختر شناسی، یعنی دستگاه زمین مرکزی منظومه شمسی رد شد.

ظهور و پیدایش رنسانس

در نیمه دوم قرن 14 در ایتالیا و در شهر فلورانس پدیده ای به نام رنسانس به وجود می آید و به بخش های مختلف اروپا اشاعه پیدا می کند . چرا با وجود کشورهایی مثل آلمان وفرانسه و امثال اینها که به شکل امروزی نبودند، چرا این پدیده در ایتالیا رخ داده است ؟ درذیل دلایل مختلفی را که در این زمینه مطرح کرده اند که رنسانس در ایتالیا اتفاق افتاده است،بیان شده است :

پایگاه مسیحیت در روم بود ولی به مرور زمان نفوذ کلیسا قدرت قبلی خود را در ایتالیا از دست می دهد و تحت فشار شاهان فرانسه در اواخر قرون وسطی دربار پاپ از روم به آونیوم در فرانسه منتقل می شود . بنابراین نفوذ کلیسا در ایتالیا کمتر می شود .

به مرور زمان، زبان رسمی و علمی در اروپا زبان لاتینی می شود. زبان های مثل اسپانیایی، ایتالیایی و فرانسوی در مقایسه با زبانی مثل آلمانی نسبت به هم دارای قرابت و نزدیکی زیادی هستند. بسیاری از آثار دوران یونان باستان به زبان لاتینی ترجمه شده بود و زبان لاتینی به زبان ایتالیایی نزدیکتر از دیگر زبان ها بود. بنابر این ایتالیایی ها راحتتر می توانستند با ترجمه های آثار یونانی ارتباط برقرار کنند .

مقر اصلی تمدن روم و امپراطوری روم درایتالیا بود . روم شرقی و بیزانس در حوزه شرقی اروپا و بالکان و سوریه بود و امپراطوری روم غربی در ایتالیا و فرانسه و آلمان بود اما مرکزیت آن در ایتالیا بود. بنابر این مردم ایتالیا به یونان و روم باستان نزدیکتر بودند چون امپراطوری روم در ایتالیا قرار داشت .

بنابر این با توجه به مجموعه این دلایل پدیده رنسانس در ایتالیا اتفاق می افتد .

رنسانس یعنی قبول نداشتن کلیسا و عقاید آن و بازگشت به یونان و روم باستان است. در یونان و روم باستان اصالت با انسان بوده است. برای برگشت به یونان و روم باستان باید در تمام مسائل از جمله هنر و ادبیات و فلسفه باید به همان روش عمل نمود. بنابر این باید به آثار همان زمان رجوع کرد و چون آثار یونان به لاتینی ترجمه شده و ایتایایی ها با توجه به قرابت زبانشان به زبان لاتینی راحتترمی توانستند زبان لاتینی را فرا گیرند اینها زودتر از بقیه توانستند به آثار یونانی دست پیدا کنند.

4-2

دستگاه خورشید مرکزی خورشید کوپرنیک

نیکلا کوپرنیک

(1543-1473)

ریاضیدان

اخترشناس، حقوقدان و اقتصادان با استعدادی بود که در نزد مردم بسیار محترم بود. اصلیت وی لهستانی بود و برای ادامه تحصیل به ایتالیا رفت. کوپرنیک نخستین کسی بود که در دوران رنسانس، انقلاب بزرگی را در زمینه اخترشناسی برپا می کند. کوپرنیک به مسئله حرکت دورانی افلاطون در مورد اجرام آسمانی بسیار علاقه مند بود و در این زمینه تلاش های بسیار انجام داد. کوپرنیک معتقد بود که حرکت اجرام آسمانی مانند ستاره ها، سیارات و ماه یک حرکت دورانی(دایره ای) و یا ترکیبی از حرکات دورانی است. زیرا در حرکات دورانی، جرم در یک دوره مشخص و ثابت به حالت و وضعیت قبلی خود برمی گردد. کوپرنیک با مشاهدات و تحقیقات گسترده و محاسبات دقیق به این نتیجه رسید که اگر حرکت سیارات با حرکت دوره ای زمین در ارتباط باشد، و حرکت دوره ای سیارات را بر اساس گردش آن ها به دور خورشید محاسبه کنیم به این نتیجه می رسیم که علاوه بر نظم و ارتباط میان آن ها(منظور حرکت دورانی زمین و خورشید مرکزی) و ترتیب حاکم بر مدار های سیارات، حرکت دورانی این اجرام با هم در ارتباط می باشند. به طوری که تغییر در هر یک از این مدار ها باعث در هم فرو ریختن اجرام و در نتیجه منظومه می شود.

سرانجام کوپرنیک منظومه خود را تدوین کرد که منظومه وی با منظومه زمین مرکزی بطلیموس که مورد قبول عامه مردم (از جمله کلیسا) آن دوره بود، مغایرت داشت.

وی در منظومه خود خورشید را مرکز قرار داد که زمین و دیگر سیارات به دور آن در حال حرکت هستند. نیکلا منظومه خود را بر اساس چند فرض بنیان نهاد:

مرکزیِ هندسی و دقیق برای مدار اجرم آسمانی وجود ندارد.

خورشید در مرکز قرار دارد و زمین و دیگر سیارات به دور آن حرکت می کنند.

زمین دیگر مرکز جهان نیست. زمین علاوه بر حرکت گردشی به دور خورشید، به دور خود نیز می چرخد.

حرکت خورشید در آسمان بر اساس حرکت دوره ای زمین می باشد.

حرکت ظاهری اجرام آسمانی در آسمان تنها بر اساس حرکت خود آن ها نیست، بلکه این حرکت ها با حرکت دوره ای زمین نیز در ارتباط می باشند.

کوپرنیک نظر داد که گردش زمین به دور خود یک شبانه روز به طول می انجامد.

کوپرنیک تلاش می کرد تا نظریه خود را از طریق ریاضیات اثبات کند. وی با محاسبات خود به این نتیجه رسید که هرچه قدر از سیارات دور به خورشید نزدیک شویم، بر سرعت گردش آن ها افزوده می شود. زحل که دورترین سیاره آن زمان بود، یک دور یکنواخت خود را به مدت 29.5 سال و سپس مشتری این دوره را در 11.8 سال می پیماید. بعد از مشتری نوبت به مریخ می رسد که این دوره را در مدت 687 روز و زهره 224 روز و عطارد 88 روز سپری می کنند. البته این مقادیر را کوپرنیک محاسبه کرده است و اختلاف این مقادیر با مقادیر امروزی ناچیز است. این محاسبات بخشی از اثبات تئوری کوپرنیک با استفاده از هندسه بود.

مزیت تئوری کوپرنیک آن بود که وی با استناد به نظریه خورشید مرکزی به نتایجی دست یافت که برخی از این نتایج در نظریه بطلیموسی امکان پذیر نبود.

مهمترین این نتایج عبارتند از:

الف) محاسبه اندازه مدار سیارات که به دور خورشید می گردند.

ب) محاسبه دوره تناوب گردش سیارات به دور خورشید.

ج) بدست آوردن سرعت نسبی حرکت دورانی سیارت.

د) مشخص کردن حرکت زاویه ای سیارات و موضع آن ها در آسمان. که این نتیجه در هر دو تئوری کوپرنیک و بطلیموس وجود داشت.

بر این اساس بود که کوپرنیک به این نتیجه رسید که میان مدار های سیارات و جایگاه آن ها ارتباطی وجود دارد؛ طبق گفته خود هرگونه تغییر مکانی در هر قسمت از آن باعث به هم خوردن قسمت های دیگر و همه جهان می شود)). کوپرنیک مدعی بود که برتری نظریه او در زیبایی و سادگی آن است. وی در این رابطه در کتاب خود، ""درباره گردش افلاک آسمانی"" می گوید((در میانه همه خورشید بدون حرکت می پاید. به راستی، چه کسی در این معبد عظیم و زیبا، منبع نور را در جایی جز آنجا که بتواند همه قسمت های دیگر را بیفروزد و روشنایی بخشد، قرار می دهد؟ پس در اساس این برگزیدگی، تقارن قابل ستایش در جهان و هماهنگی بارزی در حرکت و اندازه کرات می یابیم، آن چنان که به هیچ وجه دیگری نمی توانست باشد.

تئوری کوپرنیک بنا به دلایلی به زودی مورد قبول عامه مردم قرار نگرفت. بیش از یک قرن طول کشید تا نظریه خورشیدمرکزی میان اخترشناسان مورد پذیرش قرارگیرد.

مهمترین دلایلی که علیه این نظریه مطرح شده بود:

منظومه کوپرنیکی بیشتر جنبه ریاضی، سادگی و زیبایی داشت و با مشاهدات نجومی آن زمان مطابقت نداشت و به همین دلیل مورد پذیرش عام قرار نگرفت.

یکی از ضعف هایی که کوپرنیک در اثبات نظریه خود داشت آن بود که او نمی توانست با استفاده از نظریه های پیشین، نظریه خود را اثبت کند.

یکی از دلایلی که همیشه بر ضد نظریه خورشیدمرکزی مطرح بود آنست که اگر زمین در حال حرکت می بود، بایستی به کلی منهدم شود. زیرا اگر زمین حرکت کند، آنگاه هوا، پرندگان و قطرات بارانی که به زمین می بارند، جا می ماندند. یکی از مثل هایی که مخالفین به گالیله می گفتند آن بود که اگر زمین در حال حرکت باشد، توپی که از بالای برج پیزا پرتاب می شد باید به عقب (جهت خلاف گردش زمین) جا بماند.

اما کوپرنیک می پنداشت که هوا به همراه زمین در حال حرکت است. و از طرفی وی در نظر داشت که اگر چنین می بود پس چرا دیگر اجرام آسمانی که در حال حرکتند، منهدم و نابود نمی شوند.

الگوی خورشید مرکزی کوپرنیک با عقاید و اصول ارسطو مغایرت داشت. و از طرفی چون در آن زمان کلیسا طرفدار اصول ارسطو بود، به همین دلیل نظر همه مسیحیان بر ضد کوپرنیک بود. آنان به آیات انجیل استناد می کردند و می گفتند که معمار و طرح خلقت جهان بر اساس منظومه و تئوری بطلیموس است. به همین دلیل سازمان تفتیش عقیده، کتاب کوپرنیک را که مخالف با کتاب مقدس بود، ممنوع اعلام کرد.

اگر چه نظریه خورشید مرکزی کوپرنیک با نظریه زمین مرکزی بطلیموس از نظر علمیِ مشاهده نجومی سازگار بود اما از نظر فلسفی مغایرت داشت. چون کوپرنیک چارچوب مرجع خود را از زمین به خورشید منتقل کرده بود. و این انتقال چارچوب از نظر فیزیک سینماتیکی امروزی کاملا صحیح می باشد.

5-2

قوانین کپلر

کوپرنیک با قرار دادن خورشید در مرکز منظومه شمسی توصیف بسیار ساده تر و توضیح طبیعی تری در باره برخی از خصوصیات حرکت سیاره ای به دست داد. هرچند طرح کوپرنیک بسیار ساده تر از طرح بطلمیوس بود، اما چون کوپرنیک نیز به تقدس دایره ها اعتقاد داشت، به همان اندازه بطلمیوس از مدارهای تدویر و نظایر آن استفاده کرد. تنها تفاوت دو دستگاه این بود که یکی زمین را مرکز حرکت سیارات می دانست و دیگری خورشید را. با آنکه ستاره شناسان از پذیرش دستگاه خورشید مرکزی بطلمیوس اجتناب می کردند، اما این دستگاه تاثیر خود را بر اندیشه آنان گذاشته بود و بحث و جدل در مورد آن روز به روز بیشتر می شد.

این مجادلات باعث شد که منجمین اطلاعات رصدی بیشتری و دقیق تری به دست آورند. تیکو براهه این اطلاعات را جمع آوری کرد و اعتقاد داشت که همه ی سیارات بجز زمین به دور خورشید می گردند و خورشید همراه سیارات به دور زمین می چرخد. در این دوران یوهان کپلر (1571-1630) به عنوان دستیار نزد تیکو براهه در رصد خانه ی پراگ مشغول کار شد.

پس از کوپرنیک ، کپلر نخستین منجم نامداری بود که نظریه مرکزیت خورشید را اتخاذ کرد ، اما معلوماتی که تیکو براهه ثبت کرده بود نشان داد که این نظریه به صورتی که کوپرنیک بدان بخشیده بود ، نمی تواند کاملا صحیح باشد. با این وجود ظرفداری کپلر از دستگاه خورشید مرکزی کوپرنیک مورد پسند تیکو برهه نبود. هنوز یکسال از همکاری این دو نگذشته بود که تیکو براهه فوت کرد و تمام رصدهایی را که جمع آوری کرده بود به عنوان ارثیه ای ارزشمند برای کپلر باقی گذارد.

پس از مرگ تیکو براهه، کپلر به توده ی عظیمی از رصدهای بسیار دقیق در حرکت سیارات دست یافت. بعداً مسئله به این صورت در آمد که الگویی برای حرکت سیارات ارائه دهد که دقیقاً با مجموعه رصدهای انجام شده مطابقت کند.

بدین ترتیب کپلر نیاز داشت که ابتدا به کمک تخیل جواب موجهی را حدس بزند و سپس با پشتکار، کوهی از محاسبات کسل کننده را انجام دهد تا حدس خود را تایید یا رد کند.

توفیق بزرگ کپلر همانا کشف سه قانون حرکت سیارات است دو تا از این قوانین را وی در 1609 و سومی را در 1619 انتشار داد .

قانون اول کپلر یا قانون بیضوی ها

مدار هر سیاره به شکل یک بیضی است که خورشید در یکی از کانونهای آن قرار دارد .

که میتوان از این مطلب این را نتیجه گرفت که فاصله سیاره تا خورشید به لحاظ واقع بودن بر مدار بیضی دارای حداقل و حداکثر است. کپلر بیش از 20 سال برای درک چگونگی مدارات سیارات زحمت کشید او مدلهای مختلفی را امتحان نمود ولی سرانجام نشان داد که صفحه مداری سیاره ها از خورشید می گذرد و کشف کرد که شکل مداری سیارات به صورت بیضی است .این قانون در سال 1609 میلادی انتشار یافت.

قانون دوم کپلر یاقانون سطح معادل

خط مستقیم واصل سیاره و خورشید (شعاع حامل یک سیاره)، در فواصل زمانی مساوی مساحتهای مساوی را در فضا جاروب می کند.

یعنی برای مثال در شکل سیاره ای در مدت 1 ماه از Aبه B می رود . مدت زمانی که از Cبه D می رود نیز یک ماه است اما اکنون از خورشید دورتر است بنابراین فاصله A تا B باید بیشتر باشد تا سیاره در همان مدت یک ماه مساحتی برابر با مساحت اول را جاروب کند . به همین دلیل سیاره هنگامی که به خورشید نزدیکتر است با سرعت بیشتری حرکت می کند. برای فهم بهتر اینجا را کلیک کنید .

قانون سوم کپلریا قانون هارمونیک

نسبت مجذور زمان تناوب گردش دو سیاره برابر است با نسبت مکعب نیم قطر اطول آنها کپلر برای بدست آوردن این فرمول 7 سال تلاش کرد . در آن زمان فاصله واقعی میان خورشید و سیارات معلوم نبود اما محاسبه نسبت فاصله یک سیاره تا خورشید به فاصله زمین تا خورشید میسر بود . مثلا کپلر می دانست که نیم قطر اطول مدار مریخ تقریبا 1.5 برابر نیم قطر اطول مدار زمین است . حال او متوجه شد اگر در هر سیاره نیم قطر اطول را به توان 3 و دوره گردش را به توان 2 برسانیم . دو رقم بدست آمده باهم برابر می شوند و فقط اختلافهای اندکی برای برجیس (مشتری) و کیوان (زحل) دیده می شود.

در زمان کپلر دو قانون اول فقط در مورد مریخ قابل اثبات بود . در مورد سایر سیارات رصد ها با آن قوانین سازش داشت ، منتهی چنان نبود که آنها را قطعا محقق سازد و مدتها گذشت تا دلایل قطعی در تایید آنها بدست آمد .

کشف قانون اول ، یعنی اینکه سیارات روی مدارات بیضوی حرکت می کنند ، بیش از آنکه برای مردم امروز به آسانی قابل تصور باشد مستلزم کوشش در رها ساختن گریبان خود از چنگ سنتها بود . تنها نکته ای که همه ی ستاره شناسان در آن خصوص با هم توافق داشتند این بود که همه ی حرکات سماوی ، دورانی است یا از حرکات دورانی ترکیب شده است .

قرار دادن بیضی به جای دایره ، مستلزم رها کردن آن تمایل زیباشناختی بود که از زمان فیثاغورث به بعد بر نجوم حکومت کرده بود . دایره شکل کامل و افلاک سماوی اجسام کامل شناخته می شدند _ که در اصل مقام خدایی داشتند و حتی در آثار افلاطون و ارسطو نیز رابطه ی نزدیکی با خدایان دارند . واضح به نظر می رسید که یک جسم کامل باید بر یک مدار کامل حرکت کند . به علاوه چون اجسام آسمانی آزادند ، یعنی بی اینکه کشیده یا رانده شوند حرکت می کنند ، پس حرکت آنها باید طبیعی باشد و تصور اینکه دایره طبیعی است و بیضی چنین نیست امر آسانی بود . بدین ترتیب بسیاری از باورهای ذهنی عمیق می بایست منسوخ و مطرود گردد تا قانون اول کپلر بتواند مورد قبول واقع شود .

قانون دوم مربوط به سرعت متغیر سیاره در نقاط مختلف مدار خویش است. بنابراین سیاره در نزدیک ترین فاصله ی خود به خورشید ، بیشترین سرعت را دارد و در دورترین فاصله ی خود از خورشید ، کمترین سرعت را .

این نکته هم باز سبب حیرت می شد زیرا که وقار و متانت سیاره مغایر این بود که گاهی شتابان و گاهی خرامان راه برود !

قانون سوم از این لحاظ مهم بود که حرکت سیارات مختلف را نسبت به هم می سنجید . قانون سوم می گوید که اگر r فاصله ی متوسط یک سیاره نسبت به خورشید و Tطول سال آن باشد . پس r^3/T^2 در مورد همه ی سیارات یک اندازه است . این قانون ( تا آنجا که به منظومه ی شمسی مربوط می شود ) دلیل قانون جادبه ی نیوتن قرار گرفت

نتیجه: آنچه که کپلر انجام داد، از جزئیات یعنی رصدهای موضعی، به کلیات یعنی مسیر حرکت سیارات دست یافت. سه قانون کپلر از رویدادهای بسیار مهم علم است که بطور کامل تقدس دایره ها را در هم شکست و نظریه کپرنیک را از حمایت موثری برخوردار کرد. این قوانین نشان داد که اگر خورشید به عنوان مرجع در نظر گرفته شود، حرکت سیارات را می توان به آسانی توصیف کرد. اما اشکال این قوانین آن بود که صرفاً تجربی بود، یعنی فقط مسیر حرکت مشاهده شده را بیان می کردند، بی آنکه هیچگونه تعبیر نظری در باره ی آنها به دست بدهند. یا در مورد منشاء این قواعد توضیح نمی داد.

همزمان ارائه این قوانین توسط کپلر، واقعه ی بزرگی در شرف تکوین بود. گالیله در زمان ارائه این قوانین به حرکت اجسام، آونگ، نور ... می اندیشید و دست به آزمایشهای سرنوشت سازی می زد. بطور قطع این دو نفر در شکل گیری اندیشه های نیوتن نقش برجسته ای داشتند.