* مطالب علمی *
ایساتیس
آقاشیر
.: شهر عشق :.
جملات زیبا
تعقل و تفکر
دکتر رحمت سخنی
بیگانه ، دختری در میان مردمان
تا ریشه هست، جوانه باید زد...
اس ام اس عاشقانه
خاطرات خاشعات
اس ام اس سرکاری اس ام اس خنده دار و اس ام اس طنز
وسوسه عقل
پرهیزکار عاشق است !
فروش و تعمیر موبایل در استان یزد
آموزش
وبلاگ تخصصی کامپیوتر
هک و ترفند
فروش و تعمیر موبایل در استان یزد
انجمن فیزیک پژوهش سرای بشرویه
عاشقان خدا فراری و گریزان به سوی عشق و حق®
وبلاگ عشق و محبت ( اقا افشین)
باید زیست
دست نوشته های دو میوه خوشمزه
در دل نهفته ها
روزگاران(حتما یه سری بهش بزن ضرر نمی کنی)
فقط برای ادد لیستم...سند تو ال
تجربه های مدیریت
سولات تخصصی امتحان دکترا دانشگاه آزاد
سولات تخصصی امتحان دکترا دانشگاه آزاد
ارزانترین و بزرگترین مرکز سوالات آزمون دکترا
عکس و اس ام اس عشقولانه
دانلود نرم افزار های روز دنیا
شاهرخ
مکانیک هوافضا اخترفیزیک
مکانیک ، هوافضا ،اخترفیزیک
وبلاگ تخصصی فیزیک و اختر فیزیک
وبلاگ تخصصی فیزیک جامدات
همه با هم برای از بین نرفتن فرهنگ ایرانی
انتخاب
فیزیک و واقعیت
ترجمه متون کوتاه انگلیسی
دنیای بیکران فیزیک
ابتدا توضیح جامعی در مورد اثر کازیمیر (Casimir Effect) می دهیم.
این اثر شامل نیرویی می شود که نه می توان آن را اثر بار و نه گرانش و رد و بدل کردن ذرات بین دو جسم دانست.
آزمایشات کازیمیر نشان می داد که این نیرو مربوط به تشدید (Resonance) میادین انرژی در میان فضای دو جسم می باشد.
از آنجاییکه اعمال این نیرو دارای اثبات ریاضی است محققان این نیرو را به ذراتی مجازی در فضای بین دو جرم نسبت دادند. اما با این وجود مشکلات زیادی در آزمایش ها بود. برای مثال محققان تا به حال متوجه نشده اند چرا این نیرو در بین دو جرم تنها هنگامی اعمال می شود که دو جرم بسیار به هم نزدیک هستند!
این نیرو در ذرات بسیار کوچک میکرونی رسانا نیروی غالب به شمار می رود زیرا در این شرایط نیروی بار بین ذرات بسیار کم خواهد بود. این مورد در آزمایش کازیمیر در سال 1948 به طور واضح دیده شد. اما سوال دیگری بعد از آن بوجود آمد که چرا این اثر تنها در خلا نمایان می شود؟
سال 1948 هندریک کازیمیر (Hendrik B.G. Casimir) فیزیکدان هلندی در آزمایشگاه فیلیپس (Philips) دو صفحه ی فلزی بدون بار را در خلا موازی یکدیگر قرار داد. نیروی مشاهده شده در این آزمایش (بین دو صفحه) تقریبا 15 درصد آن چیزی بود که او در معادلات خود پیش بینی می کرد!
بعد از این آزمایش دانشمندان نیز دریافتند این نیرو همان نیرویی است که در بین اتم های بدون بار وجود دارد. نیرویی که آن را واندروالس (Van Der Waals) نامیده بودند.
"آزمایش کازیمیر: نیروی بوجود آمده از قرار دادن دو صفحه ی موازی بدون بار در خلا"
خود کازیمیر دلیل این موضوع را متوجه نشد که چرا این صفحات تنها در خلا بین خود نیرو رد و بدل می کنند ولی آن را به مقداری به نام ارزش انتظاری (فرضی) خلا مرتبط کرد و بیان نمود از آنجا که مکان های دیگر این ارزش را ندارند پس در آنجا چنین واکنشی صورت نخواهد گرفت.
برای مثال این مقدار در مکانیک هگز – بوزون 26 گیگا الکترون ولت می باشد.
بعد از این فرضیه به سرعت فرضیه ی دیگری با نام انرژی نقطه ی صفر (ZPE) یا انرژی خلا بیان شد. دانشمندان در صدد بودند تا از مشاهداتی که داشته اند دریابند که آیا انرژی و اثرات خلا دارای یک ثابت است و جز نیروهای اولیه محسوب می شود یا نه؟
از آنجاییکه اگر این ذرات خلا وجود داشتند دارای جرم نبودند پس فرض کردند که این انرژی باید کوچکترین انرژی امکان پذیر در یک سیستم مکانیک کوانتومی باشد.
فرض بعدی از این قرار بود که هر سیستم کوانتومی خود دارای یک مقدار دارای نظم از این انرژی باشد. یعنی بین این مقادیر در سیستم های مختلف نظم و رابطه ای ریاضی برقرار باشد.
حال هرجا این مقدار انرژی به مقدار همیلتونین (Hamiltonian) برسد به آن ارزش انتظاری خلا یا انرژی خلا می گویند.
اعتقاد تئوری VMR-PCR بر این است که Casimir Effect و van der Waals force هر دو در تلاش بوده اند تا نیرو (یا انرژی ای) را پیدا کنند که جز عوامل شناخته شده نباشد.
این عامل همان خلا می باشد که طبق مدل مکانیک VMR-PCR از لحاظ نیرو یا انرژی طبقه بندی می شود.
این عامل بین دو بازه ی نیرو و انرژی قرار دارد. سرعتی که این عامل تماما از نیرو می باشد را در مدل صفر فرض کرده ایم و در سرعت مربع نور عامل کاملا انرژی می شود. اما به طور معمول و در اثر گرانش که برآیند نیروی این عامل و دافعه ی ماده است مقدار نیرو در اثرات این عامل جذری از مقدار انرژی در آن است. (مقادیر بازه ی بالا و پایین برای حد خلا تعریف نمی شوند. زیرا خلا در سرعت تقریبی ثابتی دفع و ایجاد گرانش می کند).
جرم قبل از اینکه به انرژی تبدیل شود طبق فرمول هم ارزی و ثابت مرتبط به نیرو تبدیل می شود.
در واقع VMR-PCR بیان می کند که هرجسم شتاب دار از یک ذره ی مشخص تشکیل نشده و خود از سه عامل جرم – نیرو و انرژی به نسبت سرعتش ایجاد شده که نام آن را عامل ناشناخته یا U agent (Unknown Agent) انتخاب کرده است.
اما تفاوتی که این تئوری با فرضیه های قبلی دارد در این می باشد که این نظریه مفهوم جدیدی از خلا و ذرات آن را تعریف می کند. اثر کازیمیر همراه با بیان چندی از اثرات خلا ذرات آن را دارای اسپین و انرژی و قطبیدگی و غیره می نامد. در صورتیکه VMR-PCR آن ذرات را به صورت ضد ماده با خواص محدود و و جدا از خواص مادی بیان می کند.
با همه ی این تفاسیر بزرگترین سوال فیزیک در سال 2006 این بوده است که چرا این مقدار انرژی نقطه ی صفر اشباع نمی شود و باعث یک مقدار کیهانی بزرگ نمی گردد؟
جواب VMR-PCR ساده است: به خاطر اینکه گرانش را ایجاد می کند و مطلقا از انرژی نیست.
اما قبل از اینکه بیشتر وارد تشریح امر شویم بهتر است انرژی نقطه ی صفر (ZPE) را کمی بیشتر توضیح دهیم.
همانطور که به صورت خلاصه بیان کردیم انرژی نقطه ی صفر (ZPE) کمترین مقدار انرژی ای است که یک سیستم مکانیک کوانتومی می تواند داشته باشد.
هر سیستمی مقدار انرژی نقطه ی صفر مخصوص به خود را دارد اما پایین ترین مقدار آن را به خلا نسبت می دهند.
انرژی نقطه ی صفر خلا به صورت واضحی از اثر کازیمیر نتیجه می شود و محققان احتمال می دهند راز ثابت کیهانی در این مورد نهفته باشد.
همچنان که گفتیم مقدار انرژی نقطه ی صفر در اثر کازیمیر خود مرتبط به ارزش انتظاری خلا و مقدار همیلتونین است.
گفتیم که دانشمندان همواره از خود می پرسند چرا انرژی نقطه ی صفر اگر منشایی مانند خلا دارد چرا در دنیا اشباع نمی شود.
VMR-PCR گرانش را برآیند نیروهای دافعه ی خلا و ماده می داند. اینگونه مشاهده می کنید که نیروی ایجاد شده از این اثر همان گرانش است. بنابراین دلیلی برای اشباع شدن نیست.
دلیل دوم این است که طبق مدل مکانیک VMR-PCR دفع خلا در سرعت نور انجام می شود و در این سرعت عامل را تماما نمی توان به انرژی مرتبط کرد. به مقدار جذری از انرژی کل در عامل نیز جرم وجود دارد و طبق فرمول هم ارزی به همین نسبت نیز همواره نیرو در عامل ایجاد می شود.
تا قبل از این هرگونه اثری را تنها به انرژی خلا مرتبط می ساختند زیرا این موارد حتی برای یک جرم تنها در خلا نیز اتفاق می افتاد!
هنوز هم برای فیزیکدانان این یک مسئله است که چطور خلایی را که خالی تصور می کنیم چنین اثراتی دارد؟ این اثرات را باید به کدام ذره نسبت داد؟ یک ذره ی مجازی؟
اگرچه دانشمندان در سالهای اخیر به خصوص 1980 سعی داشتند گرانش را به انرژی ربط دهند و این امر را نیز توجیه کنند اما با مشاهده ی رفتارهای دنیا فرض آنها با شکست مواجه شد.
در حال حاضر نیز 3 چیز در کیهان شناسی وجود دارد که کاملا مرتبط به هم هستند اما هرسه بدون پاسخ باقی مانده اند: ثابت کیهانی – انرژی خلا و انرژی نقطه ی صفر!
حال با VMR-PCR می دانیم که این اثر با آنکه مرتبط به خلا است اما نباید کاملا آن را به انرژی نسبت داد.
همچنین ماده ای در این امر دخیل نیست و این تنها کنش میان خلا (ضدماده) و ماده است.
به همین گونه توانستیم هر سه مورد را با دلایلی که فقط راز آنها نهفته در دفع خلا (ضدماده) با ماده بود توجیه کنیم.
کلمات کلیدی: ترمو دینامیک
مقدمه:
همه کم و بیش درکی شهودی از مفاهیم گرما ، فشار و حتی انرژی درونی داریم اما به نظر می رسد در خصوص مفهوم فیزیکی آنتالپی این گونه نباشد! برای نزدیک شدن به این درک ، قانون اول ترمودینامیک را در نظر بگیرید. همان طور که می دانیم این قانون در واقع بیانی است از قانون پایستگی انرژی و با این توضیح اضافی که گرما نیز صورتی از انرژی است. این قانون را به طور کمی به صورت dQ=dU+dW بیان می کنند که در آن d معرف تفاضل یا اختلاف است. همچنین کمیت های W,U,Q به ترتیب گرما ، انرژی درونی و کار را نشان می دهند. هر گاه در فشار ثابت حجم دستگاهی به مقدار کوچکی تغییر کند، دستگاه به اندازه ی dW=PdV روی محیط کار انجام می دهد و یا بر عکس از طرف محیط روی دستگاه کار انجام می شود. حال فرض کنید در یک فرایند هم فشار انرژی درونی و حجم دستگاهی تغییر کند. در این صورت به کمک قانون اول ترمودینامیک و رابطه ی کار در فرایند هم فشار به سادگی به رابطه ی (dQ=d(U+PV می رسیم که کمیت داخل پرانتز یعنی U+PV را با H نشان می دهند و آن را آنتالپی می نامند. در این صورت داریم dQ=dH . بنابراین ، هرگاه فرایندی هم فشار بر روی دستگاهی انجام شود گرمای داده شده یا گرفته شده از دستگاه با تغییر انتالپی آن برابر است. از همین رو آنتالپی را محتوای گرمایی دستگاه نیز می نامند! از آنجا که در شیمی و مهندسی بیشتر فرایندها در فشار ثابت انجام می شود مفهوم آنتالپی کاربرد زیادی دارد.
تعریف آنتالپی
آنتالپی سیستم، تابعی ترمودینامیکی است که با مجموع انرژی درونی سیستم و حاصلضرب حجم در فشار آن (در فشار ثلبت) در محیط سیستم، هم ارز است. به عبارت دیگر گرمای جذب شده بوسیله واکنشی که در فشار ثابت انجام میگیرد، برابر با تغییر آنتالپی سیستم است. آنتالپی، همانند انرژی داخلی، تابعی از حالت سیستم و مستقل از راهی است که به آن حالت میرسد.
حالت های ماده
هر سیستمی اعم از جامد، مایع و گاز شامل اتمها یا یونها و یا مولکولهای ساده ای است که بهم دو نوع نیروی مختلف اعمال می کنند:
1- جاذبه ی بین ذرات
2- انرژی جنبشی
جاذبه ی بین ذرات
جاذبه ی بین اتمها، یونها و ملکولها به موارد زیر تقسیم می شود:
لف: کنش یونی
ب: قید هیدروژنی ( بویژه کنش دو قطبی)
ج: کنش دو قطبی
د: تحریک شدن ناپایدار کنش دو قطبی
انرژی جنبشی
انرژی جنبشی طبق رابطه ی زیر داده می شود:
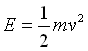
انرژی جنبشی مستقیماً با دمای مطلق متناسب است، زیر سرعت مولکولی (u) یک گاز کامل از رابطه زیر به دست می آید:
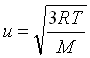
M جرم مولی
حالت های جامد، مایع و گاز
در حالت جامد، نیروی جاذبه مولکولی بر نیروی جنبش مولکولی غلبه دارد و موجب می شود اتمها یا مولکولها در مجاورت یکدیگر باقی بمانند.
-
در اینجا هندسه ی ثابتی در همسایگی اتمها وجود دارد
-
مجموعه ی اتمها دارای شکل و حجم معینی هستند
در مایعات انرژی جنبشی بیشتر از حالت جامدات است. این انرژی آن اندازه نیست که مولکولها را از هم جدا کند و به اندازه هم کم نیست که مولکولها در محاورت یکدیگر ثابت بمانند.
-
در اینجا هندسه ی ثابتی در همسایگی اتمها وجود ندارد
-
مجموعه ی اتمها دارای شکل ثابتی نیست، اما دارای حجم ثابتی هستند
-
جامد و ماده هر دو حالتهای فشرده ی ماده هستند.
در گازها انرژی جنبشی در یک نقطه بیشتر از نیروهای جاذبه است، بطوریکه اتمها و مولکولها کاملاً از یکدیگر جدا می شوند.
-
مجموعه اتمها منبسط می شوند و حجم فضایی را که در آن قرار دارند، اشغال می کنند.
انرژی درونی و تبادل حرارتی
اگر به یک سیستم انرژی گرمایی (q) داده شود، انرژی درونی آن (U) افزایش می یابد، و اگر سیستم روی محیط کار (w) انجام دهد، انرژی درونی آن کاهش می یابد بطوریکه:
dU = dq + dw
که در آن کار انجام توسط سیستم منفی در نظر گرفته می شود.
برای یک سیستم پتانسیلی که کار انبساطی انجام دهد، آنتالپی (H) آن بصورت زیر تعریف می شود.
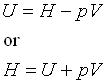
در اینجا P فشار و V حجم سیستم است.
PV نوعی انرژی است که به حاصلضرب فشار در حجم سیستم مربوط می شود و کار انجام می دهد.
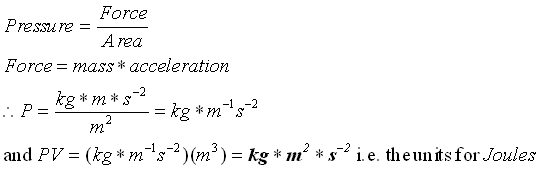
در یک فشار ثابت، تغییرات آنتالپی (dH) یک سیستم برابر با گرمای اعمال شده بر سیستم.
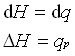
![]()
بنابراین برای تغییرات جزئی سیستم داریم:
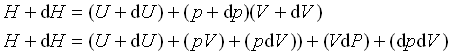
dpdV حاصلضرب دو مقدار کوچک است که با صرف نظر کردن از آن خواهیم داشت:
![]()
![]()
بنابراین
![]()
با جایگذاری (dq + dw) بجای dU خواهیم داشت
![]()
به شرط بودن فشار ، dp برابر صفر خواهد شد و داریم:
![]()
در نهایت به قسمت dw توج کنید. اگر سیستم هیچگونه کار الکتریکی یا مکانیکی و.. انجام ندهد، تنها کاری که می تواند انجام دهد، کار ناشی از pV (انبساط) است. در صورت ثابت بودن فشار، کار ناشی از انبساط تنها به pdV مربوط خواهد شد.، و هرگاه کار انجام شده منفی باشد، pdV نیز منفی خواهد شد.
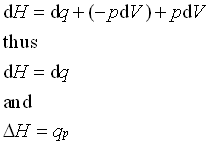
برای یک سیستم در فشار ثابت، تغییرات آنتالپی سیستم برابر با گرمایی است که به سیستم داده می شود.
تبادی حرارتی و تغییر حالت
اگر به مقدار حرارت کسب شده و دمای ماده بررسی شود، می توان ظرفیت گرمایی مواد را اندازه گیری کرد.
-
برای مثال مقدار حرارت لازم برای آنکه فشار در طی یک فرایند ثابت بماند.
-
ظرفیت گرمایی در فشار ثابت Cp و گرمای لازم بصورت زیر تعریف می شود.
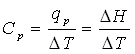
-
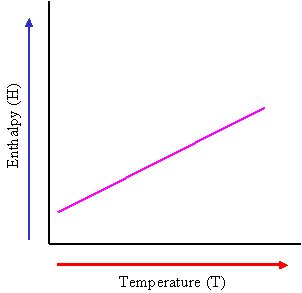
بنابراین Cp برابر شیب نمودار آنتلپی (H) و دما (T) است.
برای بسیاری از مواد، ظرفیت گرمایی در فشار ثابت در هر دمای اختیاری T برابر است با شیب منحنی نمودار آنتالپی و دما.
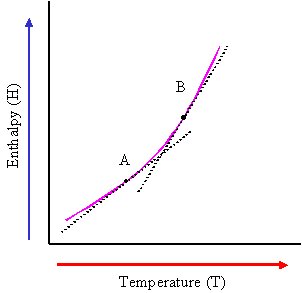
-
بنابراین روابط بیشتر بصورت های زیر خواهد بود:
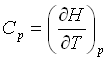
و بالعکس، تغییرا آنتالپی برای رفتن از دمای (T1) به دمای (T2) تابع ظرفیت گرمایی ماده است.
-
هنگامیکه Cp در یک محدوده ثابت باشد، خواهیم داشت:
![]()
-
در حالت کلی که ظرفیت گرمایی Cp تابع دما است با انتگرال گیری از Cp بصورت تابعی از دما خواهیم داشت:
![]()
بنابراین ظرفیت گرمایی در فشار ثابت مشتق آنتالپی نسبت به دما است. و تغییرات آنتالپی انتگرال ظرفیت گرمایی در فشار ثابت است.
حالت تغییرات آب
اگر آب را از حالت جامد آن (یخ) از 25°C- مورد بررسی قرار دهیم، و به آن تا +125°Cحرارت بدهیم، (در فشار یک آتمسفر) داده های به دست آمده شبیه نمودار زیر خواهد شد.
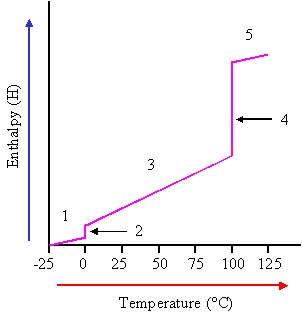
در تمام مراحل این فرایند، فشار ثابت است.
1- بین منفی 25°C تا o°C شیب نمودار ثابت است.
Cp=37.6 J mol-1 K-1
2- در o°C چنین به نظر می رسد که گرمای ویژه نامحدود است.
اما آزمایش نشان می دهد که گرمای ذوب (تابع آنتالپی یخ) 6.01 kJ mol-1 است.
3- بین صفر تا 100 درجه ی سانتیگراد ظرفیت گرمایی آب برابر است با:
75.2 J mol-1 K-1
4- دو باره در 100 ئرجه ی سانتیگراد چنین به نظر می رسد که گرمای ویژه ی آب ( آب جوش) بی نهایت است. اما تجربه نشان می دهد که با گرفتن مقداری گرما از حالت مایع به حالت بخار در می آید. و برای آنتالپی تبخیر داریم:
40.7 kJ mol-1
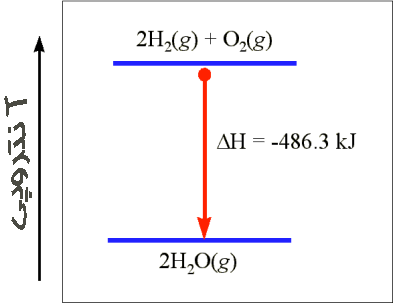
حال به فرایند زیر توجه کنید که در آن اکسیژن و هیدروژن با یکدیگر ترکیب شده و آب تولید می کنند. در اینجا نیز فشار ثابت است، اما آنتالپی سیستم تغییر می کند.
در این فرایند که تبدیل گاز به مایع است فشار ثابت می باشد و آنتالپی سیستم تغییر می کند.
کلمات کلیدی: ترمو دینامیک
| تغییرات آنتالپی مربوط به تراکم یونهای گازی شکل مثبت و منفی به یک بلور را انرژی شبکه آن بلور مینامند. برای مثال انرژی شبکه کلرید سدیم 788- کیلو ژول بر مول است. |
  |
علامت انرژی شبکه
از آنجا که در اینگونه فرآیندها همواره انرژی آزاد میشود، تمام انرژیهای شبکه علامت منفی دارند. برعکس انرژی مورد نیاز برای جدا کردن یونهای یک مول بلور برابر انرژی شبکه با علامت مثبت است. 
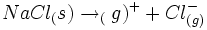
اهمیت انرژی شبکه با استفاده از تحلیل "بور - هابر"
اهمیت انرژی شبکه را با استفاده از روش تحلیلی که توسط ماکس بور و فرتینر هابر در سال 1917 جدا از یکدیگر تکوین یافت، میتوان مشاهده کرد. چرخه "بور - هابر" برای تولید کلرید سدیم از عناصر مربوط مورد استفاده قرار میگیرد. تحلیل "بور - هابر" بر اساس قانون هس قرار دارد. قانون هس میگوید که تغییر آنتالپی هر نوع واکنش شیمیایی مقداری است ثابت ، خواه واکنش در یک مرحله و خواه در چند مرحله صورت گیرد.
تغییر آنتالپی تولید یک مول 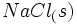 در یک مرحله از
در یک مرحله از 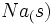 و
و 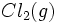 ، آنتالپی تشکیل این ترکیب است.
، آنتالپی تشکیل این ترکیب است.
مراحل تشکیل 
میتوانیم تولید یک مول  را از
را از 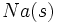 و
و  در چند مرحله تصور کنیم. جمع جبری مقادیر ΔH در این مراحل باید بر اساس قانون هس برابر آنتالپی تشکیل
در چند مرحله تصور کنیم. جمع جبری مقادیر ΔH در این مراحل باید بر اساس قانون هس برابر آنتالپی تشکیل  که مراحل ΔH واکنش در یک مرحله است، باشد. مراحل مزبور به قرار زیر است.
که مراحل ΔH واکنش در یک مرحله است، باشد. مراحل مزبور به قرار زیر است.
-
فلز سدیم بلورین تصعید میشود و به اتمهای گازی سدیم تبدیل میگردد. در این عمل برای هر مول سدیم 108 کیلو ژول انرژی جذب میشود. ( انرژی تصعید سدیم )
-
نیم مول از مولکولهای
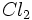 گازی تفکیک میشود و به یک مول اتم Cl گازی تبدیل میگردد. آنتالپی تفکیک
گازی تفکیک میشود و به یک مول اتم Cl گازی تبدیل میگردد. آنتالپی تفکیک  که انرژی پیوندی Cl - Cl نیز نامیده میشود، برابر 243Kj برای هر مول
که انرژی پیوندی Cl - Cl نیز نامیده میشود، برابر 243Kj برای هر مول 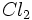 است. از آنجا که تنها نیم مول
است. از آنجا که تنها نیم مول 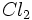 در این عمل مورد نیاز است، انرژی تفکیک نیر نصف میشود. ( 122+ Kj )
در این عمل مورد نیاز است، انرژی تفکیک نیر نصف میشود. ( 122+ Kj ) -
اتمهای سدیم گازی یونیزه میشوند و به یونهای سدیم گازی تبدیل میگردند. مقدار انرژی لازم همان انرژی اولین یونش سدیم است. ( 496+ Kj )
-
اتمهای کلر گازی الکترون میگیرند و به یونهای کلرید گازی تبدیل میشوند. تغییر آنتالپی برای هر مول
 ، برابر اولین الکترون خواهی کلر است. در این فرایند انرژی آزاد میشود، (349 - کیلو ژول) این اولین مرحلهای است که در آن انرژی آزاد میشود. اما انرژی آزاد شده ، انرژیهای مورد نیاز مراحل پیشین را تامین نمیکند.
، برابر اولین الکترون خواهی کلر است. در این فرایند انرژی آزاد میشود، (349 - کیلو ژول) این اولین مرحلهای است که در آن انرژی آزاد میشود. اما انرژی آزاد شده ، انرژیهای مورد نیاز مراحل پیشین را تامین نمیکند. -
در آخرین مرحله ، یونهای گازی بصورت یک مول بلور کلرید سدیم متراکم میشوند. تغییر آنتالپی این عمل یعنی انرژی شبکه
 برابر 788- کیلو ژول است که نشانه آزاد شدن انرژی است. روشن است که بیشتر انرژی آزاد شده در کل واکنش ، از این مرحله ناشی میشود. یعنی این مرحله است که زمینه انجام این فرآیند را از نظر انرژی مساعد میکند.
برابر 788- کیلو ژول است که نشانه آزاد شدن انرژی است. روشن است که بیشتر انرژی آزاد شده در کل واکنش ، از این مرحله ناشی میشود. یعنی این مرحله است که زمینه انجام این فرآیند را از نظر انرژی مساعد میکند.
اگر معادلات گرما شیمیایی مراحل 1 تا 5 را جمع کنیم، نتیجه عبارت از معادله آنتالپی تشکیل خواهد بود، که به صورت زیر است:
خواهد بود، که به صورت زیر است:
مورد استفاده چرخه "بور - هابر"
از چرخههای "بور - هابر" ، برای تحلیل فرآیندها و پی بردن به اینکه تغییر در یک مرحله چه اثری در کل فرآیند خواهد داشت، استفاده میکنند. این چرخهها را میتوان برای محاسبه تغییر آنتالپی یکی از مراحل یا کل فرآیند نیز بکار برد.
مقدار انرژی شبکه
بطورکلی مقدار انرژی شبکه به دو عامل بستگی دارد:
بار یونها
هنگام تشکیل بلور هر چه بار یونهای بوجود آورنده بلور بیشتر باشد، انرژی شبکه زیادتری آزاد میشود. زیرا هر چه قدر مطلق بارهای مثبت و منفی بزرگتر از هم باشد، به همان نسبت جاذبه بین آنها قویتر و انرژی آزاد شده بیشتر است.
اندازه یونها
هر چه فاصله دو بار ناهمنام کمتر باشد، نیروی جاذبه قویتر و انرژی آزاد شده بیشتر خواهد بود. لذا انرژی شبکه بلور ناشی از یونهای کوچکتر که توانایی نزدیکتر شدن دارند، بیش از انرژی شبکه بلور ناشی از یونهای بزرگتر است، به شرط اینکه بار یونهای ترکیب یکسان باشد. از آنجا که یون  کوچکتر از یون
کوچکتر از یون 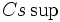 است، اختلاف انرژی شبکه (NaCl (-788Kj/mol و (CsCl (- 669Kj/mol شگفت آور نیست.
است، اختلاف انرژی شبکه (NaCl (-788Kj/mol و (CsCl (- 669Kj/mol شگفت آور نیست.
کلمات کلیدی: ترمو دینامیک
| گرمای جذب شده بوسیله واکنشی که در فشار ثابت انجام میگیرد برابر با تغییر آنتالپی است. آنتالپی ، همانند انرژی داخلی ، تابعی از حالت سیستم و مستقل از راهی است که به آن حالت میرسد. یعنی تابع حالت و یک کمیت شدتی است. |
کار در واکنشهای شیمیایی
برای واکنشهای شیمیایی عادی ، کار عموما ناشی از تغییرات فشار ، حجم است. اگر سیستم (به علت گاز) منبسط شود، در برابر فشار اتمسفر کار انجام میدهد واین نمونهای از کار فشار - حجم است. جمله PV دارای ابعاد کار است. فشار که نیرو بر واحد سطح است، بر حسب نیوتن بر متر مربع N/m2 بیان میشود. اگر حجم بر حسب متر مکعب m3 بیان شده باشد، حاصلضرب PV عبارت خواهد بود از:
(PV=(N/m2)(m3)=N.m(J
نیوتن متر (یک ژول) یک واحد کار است، زیرا کار به صورت حاصلضرب نیرو (نیوتن) در فاصله (متر) تعریف شده است. به طریق مشابه میتوان گفت که لیتر اتمسفر نیز واحد کار است. اگر فشار ثابت بماند و حجم بر اثر انبساط از VA به VB برسد، کار انجام شده عبارت خواهد بود از:
W=P(VB-VA)=P∆V
کار انجام شده در حجم ثابت
هیچ گونه کار فشار ، حجمی نمیتواند بوسیله فرآیندی که در حجم ثابت صورت میگیرد، انجام شود، W=0 خواهد بود. پس در حجم ثابت معادله: E=Q-W∆
به صورت زیر در خواهد آمد: E=QV∆ که در آن qv کار انجام شده در حجم ثابت است.
کار انجام شده در فشار ثابت
در شیمی فرآیندهایی که در فشار ثابت انجام میگیرند، بسیار متداولتر از فرآیندهایی هستند که در حجم ثابت انجام میشوند. اگر ما توجه خود را بکار فشار - حجم متمرکز کنیم، کار انجام شده در فرآیندهایی که در فشار ثابت به صورت P∆V خواهد بود. پس در فشار ثابت معادله
: E=q-W∆ به صورت زیر در خواهد آمد:
E=qp+P∆V∆
اگر در معادله فوق qp را به دست آوریم خواهیم داشت:
که در آن ، گرمای جذب شده بوسیله سیستم در فشار ثابت است.
تابع ترمودینامیکی آنتالپی
تابع ترمودینامیکی آنتالپی ، H ، با معادله زیر معادله زیر تعریف میشود: H=E+PV
بنابراین qp=∆H
یعنی گرمای جذب شده بوسیله سسیتم در واکنش در فشار ثابت:
اعتبار قانون هس نیز براساس آنتالپی استوار است.
رابطه بین تغییرات در آنتالپی و تغییر در انرژی درونی
وقتی که برای اندازه گیریهای گرماسنجی، از گرماسنج بمبی استفاده میکنیم، اثر گرمایی در حجم ثابت اندازه گیری میشود. واکنشهای معمولی در فشار ثابت انجام میشوند. رابطه میان تغییر در آنتالپی و تغییر در انرژی داخلی برای تبدیل گرماهای واکنش در حجم ثابت qv=∆E به گرماهای واکنش در فشار ثابت qp=∆E مورد استفاده قرار میگیرد. این تغییر با توجه به تغییر حجم محصولات واکنش به عمل میآید و این تغییر در حجم مایعات و جامدات به قدری است که میتوان ان را نادیده گرفت.
اما در واکنشهایی که مواد گازی دخالت دارند، تغییر حجم اهمیت پیدا میکند فرض کنید که VqA حجم کلی واکنش دهندههایی گازی ، VqB حجم کلی محصولات گازی ، nA عمده مولهای واکنش دهندههای گاز ، np عده مولهای محصولات گازی و فشار و دما ثابت است. در این صورت E+(∆n)RT∆=∆
که در آن n∆ عده مولهای محصولات منهای عده مولهای واکنش دهندههای گازی است.
آنتالپی تشکیل
یک روش آسان برای محاسبه H∆ یک واکنش ، استفاده از مقادیر ثبت شدهای است که آتالپیهای تشکیل استاندارد نامیده میشود. آنتالپی تشکیل استاندارد (که با نماد H˚f∆ نشان داده میشود) مقدار H∆ مربوط به واکنشی است که در آن یک مول ماده در 1atm و دمای مرجع خاصی از عناصر سازنده آن در پایدارترین شکلی که در فشار 1atm و دمای مرجع دارند، تشکیل میشود. نماد ˚H∆ که مشخص کننده تغییرات آنتالپی استاندارد است، برای واکنشهایی بکار میآید که فقط شامل موادی در حالت استاندارد هستند.
کلمات کلیدی: ترمو دینامیک
| میزان کاتورگی یا بینظمی یک سیستم که به عنوان معیار خودبخودی واکنش بکار میرود، آنتروپی نامیده میشود که برحسب J/K.mol بوده و با S نمایش داده میشود. |
قانون دوم ترمودینامیک و آنتروپی
قانون اول ترمودینامیک به معرفی انرژی درونی ، U ، منجر شد. این کمیت تابع حالتی است که بر مبنای آن ، مجاز بودن یک فرآیند مورد قضاوت قرار میگیرد و بیان میدارد که فقط تحولاتی مجاز است که انرژی داخلی کل سیستم منزوی ، ثابت بماند. قانونی که ملاک خودبخودی بودن را مشخص میسازد (قانون دوم ترمودینامیک) ، برحسب تابع حالت دیگری بیان میشود. این تابع حالت ، آنتروپی ، S ، است.
ملاحظه خواهیم کرد که بر مبنای آنتروپی قضاوت میکنیم که آیا یک حالت بطور خودبخودی از حالت دیگری قابل حصول میباشد. در قانون اول با استفاده از انرژی داخلی ، تحولات مجاز مشخص میشود (آنهایی که انرژی ثابت دارند). از قانون دوم با استفاده از آنتروپی ، تحولات خودبخودی از بین همان فرآیندهایی مشخص میشود که بر مبنای قانون اول مجاز میباشد.
بیان قانون دوم
آنتروپی سیستم منزوی در یک فرآیند خودبخودی افزایش مییابد: 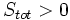
که 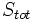 ، آنتروپی تمام قسمتهای سیستم منزوی میباشد.
، آنتروپی تمام قسمتهای سیستم منزوی میباشد.
از آنجایی که فرآیندهای برگشت ناپذیر (مانند سرد شدن شیئی تا دمای محیط و انبساط آزاد گازها) خودبخودی است، در نتیجه همه آنها با افزایش آنتروپی توام میباشند. این نکته را میتوان به این صورت مطرح کرد که در فرایندهای برگشت ناپذیر آنتروپی تولید میشود. از طرف دیگر ، در فرایند برگشت پذیر توازن وجود دارد، یعنی سیستم با محیط در هر مرحله در تعادل است. هر مرحله بسیار کوچک در این مسیر برگشت پذیر بوده و پخش نامنظم انرژی روی نمیدهد و در نتیجه آنتروپی افزایش نمییابد، یعنی در فرآیند برگشت پذیر آنتروپی ایجاد نمیشود. آنتروپی در فرآیندهای برگشت پذیر از بخشی از سیستم منزوی به بخش دیگری منتقل میگردد.
تعریف آماری آنتروپی
بر مبنای تعریف آماری ، فرض میشود که در واقع میتوانیم با استفاده از فرمول ارائه شده توسط لوودیگ بولتزمن (Ludwing Boltzmann) در سال 1896 ، آنتروپی را محاسبه کنیم: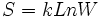
که k، ثابت بولتزمن است: 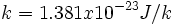
این ثابت به صورت 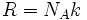 به ثابت گاز ربط دارد. کمیت W تعداد راههای متفاوتی است که سیستم میتواند با توزیع اتمها یا مولکولها بر روی حالتهای در دسترس به انرژی خاصی برسد. واحد آنتروپی با واحد k یکسان است. در نتیجه واحد آنتروپی مولی ،
به ثابت گاز ربط دارد. کمیت W تعداد راههای متفاوتی است که سیستم میتواند با توزیع اتمها یا مولکولها بر روی حالتهای در دسترس به انرژی خاصی برسد. واحد آنتروپی با واحد k یکسان است. در نتیجه واحد آنتروپی مولی ،  میباشد؛ (این با واحد R و ظرفیت گرمایی یکی است.)
میباشد؛ (این با واحد R و ظرفیت گرمایی یکی است.)
تعریف ترمودینامیکی انرژی
در روش ترمودینامیکی ، تمرکز بر روی تغییر آنتروپی در طول یک فرایند ، dS ، میباشد، نه مقدار معلق S. تعریف dS بر این مبناست که میتوان میزان پخش انرژی را به انرژی مبادله شده به صورت گرما ، در حین انجام فرایند ربط داد. تعاریف آماری و ترمودینامیکی با هم سازگار میباشند. در شیمی فیزیک این یک لحظه نشاط آور است که بین خواص تودهای (که مورد نظر ترمودینامیک است) و خواص اتمها یک ارتباط برقرار شود.
تغییر آنتروپی محیط
تغییر آنتروپی محیط را با علامت "dS نشان میدهیم. علامت پریم مربوط به محیط سیستم واقعی که در سیستم منزوی بزرگ قرار دارد، مربوط میشود. محیط را با یک مخزن حرارتی بزرگ (عملا یک حمام آب) نشان میدهیم که در دمای T باقی میماند. مقدار گرمای منتقل شده به مخزن در اثر انجام کار مانند سقوط یک وزنه را با "dq نشان میدهیم که این گرما به مخزن منتقل میشود. هرچه مقدار گرمای بیشتری به مخزن منتقل شود، حرکت حرارتی بیشتری هم در آن ایجاد میشود و از این رو ، پخش انرژی به میزان بیشتری اتفاق میافتد. از این نکته استنباط میشود که:
اگر گرما به مخزن سردی منتقل شود، کیفیت انرژی نسبت به موردی که آن گرما به مخزن گرمتری داده شود، انحطاط بیشتری خواهد داشت. در مورد اخیر میتوانیم در اثر جاری شدن گرمای "dq از یک مخزن سرد به مخزن سردتری کار استخراج کنیم، اما اگر این گرما مستقما به مخزن سردتر منتقل شود، استخراج چنین کاری امکان پذیر نیست.
نتیجه میگیریم که اگر مقدار معین انرژی به صورت گرما به مخزن گرمی داده شود، آنتروپی کمتری ایجاد میشود تا اینکه آن انرژی به مخزن سردی داده شود. سادهترین راهی که میتوان این وابستگی دمایی را به حساب آورد، چنین است: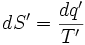
که "T دمایی است که در آن دما ، انتقال گرما صورت گرفته است. برای یک تغییر قابل اندازه گیری در دمای ثابت چنین داریم:
وقتی که مقدار زیادی حرکت حرارتی در دمای پایین ایجاد شود، تغییر آنتروپی بزرگی اتفاق میافتد. برای فرآیند آدیاباتیک:
0 = "q وقتی 0 = "S∆
این نتیجه برای هر فرآیندی ، برگشت پذیر یا برگشت ناپذیر ، صحیح است، تا زمانی که مناطق گرم محلی در محیط ایجاد نشود، یعنی زمانی این نتیجه صحیح است که محیط ، تعادل درونی خود را حفظ کند. اگر مناطقی محلی بوجود آید، انرژی از این مناطق بطور خودبخودی پخش میشود و در نتیجه آن آنتروپی تولید میشود. موقعی که یک واکنش شیمیایی با تغییر آنتالپی H∆ در سیستمی انجام میشود، گرمایی که در فشار ثابت وارد محیط میشود، برابر با 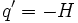 . بنابراین تغییر آنتروپی محیط برابر است با:
. بنابراین تغییر آنتروپی محیط برابر است با:
کلمات کلیدی: ترمو دینامیک



.GIF)